Area De Acero 4v1z3y
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3b7i
Overview 3e4r5l
& View Area De Acero as PDF for free.
More details w3441
- Words: 1,054
- Pages: 8
CÁLCULO DE ÁREA DE ACERO Usted está contratado para diseñar las viguetas del balcón que se muestra en la Figura. Para esto, debe encontrar el As (acero de refuerzo) requerido, expresado en número de varillas de refuerzo que debe tener la sección de las viguetas laterales y central, para que resista el momento de diseño debido a una carga distribuida en el balcón de 10 kN/m2. La sección de las viguetas tiene un ancho b= 0.1 m y una altura h= 0.3 m. Para el diseño de viguetas suponga el espaciamiento entre varillas de centro a centro igual al diámetro de la varilla. Usted debe: a) Dibujar el diagrama de momento de las viguetas (central y lateral). b) Definir el sitio de ubicación del acero de refuerzo basado en el diagrama del punto a). c) Encontrar el área de acero As basado en la metodología vista en clase y teniendo la resistencia tanto del concreto como del acero (fy). d) Mostrar un esquema de la sección trasversal con la ubicación de las barras. e) Ahora suponemos que la viga principal (que no tiene ningún refuerzo) esta empotrada y las viguetas le transfieren el momento creado por el empotramiento. Las dimensiones de la viga principal son b= 0.2m y h= 0.4m. Calcule el ángulo de torsión en grados. Tenga en cuenta que el G del concreto es de 8.3 MPa. Propiedades de los materiales para el diseño de las viguetas son las siguientes: f’c= 20 MPa. Ec= 20 GPa. fy= 240 MPa. Ea= 200 GPa.
(a) Dibujar el diagrama de momento de las viguetas (central y lateral). Cálculo de áreas colaborantes A (m2), cargas puntuales P (KN) y cargas distribuidas por unidad de longitud W (KN/m) en la loseta del balcón.
𝐴1 = 1,5 ∗ 0,85 = 1,275 𝑚2 𝐴2 = 1,5 ∗ 0,60 = 0,90 𝑚2 𝐴3 = 1,5 ∗ 0,85 = 1,275 𝑚2
𝑊𝑙𝑜𝑠𝑒𝑡𝑎 = 10
𝐾𝑁 𝑚2
𝑃1 = 10
𝐾𝑁 ∗ 1,275 𝑚2 = 12,75 𝐾𝑁 2 𝑚
𝑃2 = 10
𝐾𝑁 ∗ 0,90 𝑚2 = 9,00 𝐾𝑁 𝑚2
𝑃3 = 10
𝐾𝑁 ∗ 1,275 𝑚2 = 12.75 𝐾𝑁 𝑚2
𝑊1 =
12,75 𝐾𝑁 𝐾𝑁 = 8,50 1,50 𝑚 𝑚
𝑊2 =
9,00 𝐾𝑁 𝐾𝑁 = 6,00 1,50 𝑚 𝑚
𝑊3 =
12,75 𝐾𝑁 𝐾𝑁 = 8,50 1,50 𝑚 𝑚
Diagrama de carga distribuida, corte y momento de las viguetas central y laterales
∑ 𝐹𝑦 = 0 𝑅𝐴𝑌 − 8,50
𝐾𝑁 ∗ 1,50𝑚 = 0 𝑚
𝑅𝐴𝑌 = 12,75 𝐾𝑁 ∑ 𝑀𝐴 = 0 𝑀𝐴 − 8,50
𝐾𝑁 ∗ 1,50𝑚 ∗ 0,75𝑚 = 0 𝑚
𝑀𝐴 = 9,563 𝐾𝑁 ∗ 𝑚
∑ 𝐹𝑦 = 0 𝑅𝐵𝑌 − 6,00
𝐾𝑁 ∗ 1,50𝑚 = 0 𝑚
𝑅𝐵𝑌 = 9,00 𝐾𝑁 ∑ 𝑀𝐵 = 0 𝑀𝐵 − 6,00
𝐾𝑁 ∗ 1,50𝑚 ∗ 0,75𝑚 = 0 𝑚
𝑀𝐵 = 6,75 𝐾𝑁 ∗ 𝑚
(b) Definir el sitio de ubicación del acero de refuerzo basado en el diagrama del punto a).
Tanto para la barra central como para las laterales, el acero se ubicará en la zona superior a una distancia 𝑌𝑠 del eje neutro.
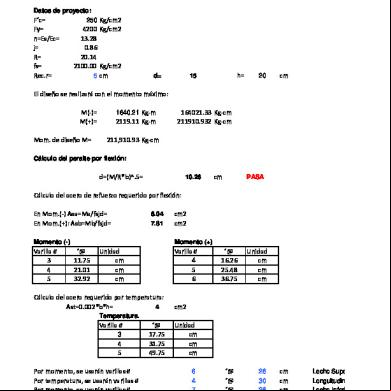
(c) Encontrar el área de acero As basado en la metodología vista en clase y teniendo la resistencia tanto del concreto como del acero (fy).
𝐴𝑠 =? 𝑑 = 25,0 𝑐𝑚 𝑏 = 10 𝑐𝑚 ℎ = 30 𝑐𝑚 𝜎𝑐 = 20𝐸𝑋𝑃 (6) 𝑃𝑎 𝐸𝑐 = 20 𝐺𝑃𝑎 𝜎𝑠 = 240𝐸𝑋𝑃 (6) 𝑃𝑎 𝐸𝑠 = 200 𝐺𝑃𝑎
C1. Factor de transformación (n): 𝑛=
𝐸𝑠 200 𝐺𝑃𝑎 = = 10 𝐸𝑐 20 𝐺𝑃𝑎
C2. Cálculo de 𝑌𝑠 𝑦 𝑌𝑐 :
𝑌𝑐 + 𝑌𝑠 = 25,00 𝑐𝑚 (Ec. 1)
C2.1 Momento estático: 𝑆𝑧𝑠𝑢𝑝 = 𝑆𝑧𝑖𝑛𝑓 10 ∗ 𝐴𝑠 ∗ 𝑌𝑠 = 10 ∗ 𝑌𝑐 ∗
𝑌𝑐 2
𝑌 10 ∗ 𝑌𝑐 ∗ 2𝑐 𝐴𝑠 = 10 ∗ 𝑌𝑠 𝑌𝑐2 𝐴𝑠 = 0,50 ∗ (Ec. 2) 𝑌𝑠
C2.2 Cálculo de las Inercias: 𝑏 ∗ ℎ3 𝐼1 = + 𝐴 ∗ 𝑑2 12 10 ∗ 𝑌𝑐3 𝑌𝑐 2 𝐼1 = + 10 ∗ 𝑌𝑐 ∗ ( ) 12 2 𝐼1 =
10 10 ∗ 𝑌𝑐3 + ∗ 𝑌𝑐3 12 4
𝐼1 =
40 ∗ 𝑌𝑐3 12
𝐼1 = 3,33 ∗ 𝑌𝑐3
𝐼2 = 𝐼𝑣𝑎𝑟 + 𝐴𝑠 ∗ 𝑌𝑠2
𝐼 = 𝐼1 + 𝐼2 𝐼 = 3,33 ∗ 𝑌𝑐3 + 0,50 ∗
𝑌𝑐2 ∗ 𝑌𝑠2 𝑌𝑠
𝐼 = 3,33 ∗ 𝑌𝑐3 + 0,50 ∗ 𝑌𝑐2 ∗ 𝑌𝑠 𝐼 = 3,33 ∗ 𝑌𝑐3 + 0,50 ∗ 𝑌𝑐2 ∗ (25 − 𝑌𝑐 ) 𝐼 = 3,33 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 − 0,50 ∗ 𝑌𝑐3 𝐼 = 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 (𝐸𝑐. 3)
PARA LAS VIGUETAS LATERALES 𝑀𝑚á𝑥 = 9,563 𝐾𝑁 ∗ 𝑚 C2.3 Fórmula de la flexión: 𝜎𝑐𝑚á𝑥. = 𝐼=
𝑀𝑚á𝑥. ∗ 𝑌𝑐 𝐼
𝑀𝑚á𝑥. ∗ 𝑌𝑐 (𝐸𝑐. 4) 𝜎𝑐𝑚á𝑥.
Ecuación 1, 2 y 3 en 4: 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 =
100 𝑐𝑚 1𝑚 ∗𝑌 𝑐 𝑁 1 𝑚2 20𝐸𝑋𝑃 (6) 2 ∗ 𝑚 1002 𝑐𝑚2
9,563 𝐸𝑋𝑃 (3) 𝑁 ∗ 𝑚 ∗
2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 = 478,15 ∗ 𝑌𝑐 2,83 ∗ 𝑌𝑐2 + 12,50 ∗ 𝑌𝑐 − 478,15 = 0 𝑌𝑐 = 10,976 𝑐𝑚 ≈ 11,00 𝑐𝑚 𝑌𝑠 = (25,00 − 11,00)𝑐𝑚 = 14,00 𝑐𝑚
C2.4 Área de acero: 𝐴𝑠 = 0,50 ∗
𝑌𝑐2 𝑌𝑠
112 𝐴𝑠 = 0,50 ∗ 𝑐𝑚2 14 𝐴𝑠 = 4,321 𝑐𝑚2 ∴ 2∅18 𝑚𝑚 (5,09 𝑐𝑚2 )
PARA LA VIGUETA CENTRAL 𝑀𝑚á𝑥 = 6,75 𝐾𝑁 ∗ 𝑚 𝑌𝑐 + 𝑌𝑠 = 25,00 𝑐𝑚 (Ec. 1) 𝐴𝑠 = 0,50 ∗
𝑌𝑐2 (Ec. 2) 𝑌𝑠
𝐼 = 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 (𝐸𝑐. 3) 𝐼=
𝑀𝑚á𝑥. ∗ 𝑌𝑐 (𝐸𝑐. 4) 𝜎𝑐𝑚á𝑥.
Ecuación 1, 2 y 3 en 4: 100 𝑐𝑚 1𝑚 ∗𝑌 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 = 𝑐 𝑁 1 𝑚2 20𝐸𝑋𝑃(6) 2 ∗ 𝑚 1002 𝑐𝑚2 6,75 𝐸𝑋𝑃 (3) 𝑁 ∗ 𝑚 ∗
2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 = 337,50 ∗ 𝑌𝑐 2,83 ∗ 𝑌𝑐2 + 12,50 ∗ 𝑌𝑐 − 337,50 = 0 𝑌𝑐 = 8,933 𝑐𝑚 ≈ 9,00 𝑐𝑚 𝑌𝑠 = (25,00 − 9,00)𝑐𝑚 = 16,00 𝑐𝑚
C2.4 Área de acero: 𝑌𝑐2 𝐴𝑠 = 0,50 ∗ 𝑌𝑠 𝐴𝑠 = 0,50 ∗
92 𝑐𝑚2 16
𝐴𝑠 = 2,531 𝑐𝑚2 ∴ 2∅14 𝑚𝑚 (3,08 𝑐𝑚2 )
(d) Mostrar un esquema de la sección trasversal con la ubicación de las barras.
VIGUETA LATERAL
VIGUETA CENTRAL
(a) Dibujar el diagrama de momento de las viguetas (central y lateral). Cálculo de áreas colaborantes A (m2), cargas puntuales P (KN) y cargas distribuidas por unidad de longitud W (KN/m) en la loseta del balcón.
𝐴1 = 1,5 ∗ 0,85 = 1,275 𝑚2 𝐴2 = 1,5 ∗ 0,60 = 0,90 𝑚2 𝐴3 = 1,5 ∗ 0,85 = 1,275 𝑚2
𝑊𝑙𝑜𝑠𝑒𝑡𝑎 = 10
𝐾𝑁 𝑚2
𝑃1 = 10
𝐾𝑁 ∗ 1,275 𝑚2 = 12,75 𝐾𝑁 2 𝑚
𝑃2 = 10
𝐾𝑁 ∗ 0,90 𝑚2 = 9,00 𝐾𝑁 𝑚2
𝑃3 = 10
𝐾𝑁 ∗ 1,275 𝑚2 = 12.75 𝐾𝑁 𝑚2
𝑊1 =
12,75 𝐾𝑁 𝐾𝑁 = 8,50 1,50 𝑚 𝑚
𝑊2 =
9,00 𝐾𝑁 𝐾𝑁 = 6,00 1,50 𝑚 𝑚
𝑊3 =
12,75 𝐾𝑁 𝐾𝑁 = 8,50 1,50 𝑚 𝑚
Diagrama de carga distribuida, corte y momento de las viguetas central y laterales
∑ 𝐹𝑦 = 0 𝑅𝐴𝑌 − 8,50
𝐾𝑁 ∗ 1,50𝑚 = 0 𝑚
𝑅𝐴𝑌 = 12,75 𝐾𝑁 ∑ 𝑀𝐴 = 0 𝑀𝐴 − 8,50
𝐾𝑁 ∗ 1,50𝑚 ∗ 0,75𝑚 = 0 𝑚
𝑀𝐴 = 9,563 𝐾𝑁 ∗ 𝑚
∑ 𝐹𝑦 = 0 𝑅𝐵𝑌 − 6,00
𝐾𝑁 ∗ 1,50𝑚 = 0 𝑚
𝑅𝐵𝑌 = 9,00 𝐾𝑁 ∑ 𝑀𝐵 = 0 𝑀𝐵 − 6,00
𝐾𝑁 ∗ 1,50𝑚 ∗ 0,75𝑚 = 0 𝑚
𝑀𝐵 = 6,75 𝐾𝑁 ∗ 𝑚
(b) Definir el sitio de ubicación del acero de refuerzo basado en el diagrama del punto a).
Tanto para la barra central como para las laterales, el acero se ubicará en la zona superior a una distancia 𝑌𝑠 del eje neutro.
(c) Encontrar el área de acero As basado en la metodología vista en clase y teniendo la resistencia tanto del concreto como del acero (fy).
𝐴𝑠 =? 𝑑 = 25,0 𝑐𝑚 𝑏 = 10 𝑐𝑚 ℎ = 30 𝑐𝑚 𝜎𝑐 = 20𝐸𝑋𝑃 (6) 𝑃𝑎 𝐸𝑐 = 20 𝐺𝑃𝑎 𝜎𝑠 = 240𝐸𝑋𝑃 (6) 𝑃𝑎 𝐸𝑠 = 200 𝐺𝑃𝑎
C1. Factor de transformación (n): 𝑛=
𝐸𝑠 200 𝐺𝑃𝑎 = = 10 𝐸𝑐 20 𝐺𝑃𝑎
C2. Cálculo de 𝑌𝑠 𝑦 𝑌𝑐 :
𝑌𝑐 + 𝑌𝑠 = 25,00 𝑐𝑚 (Ec. 1)
C2.1 Momento estático: 𝑆𝑧𝑠𝑢𝑝 = 𝑆𝑧𝑖𝑛𝑓 10 ∗ 𝐴𝑠 ∗ 𝑌𝑠 = 10 ∗ 𝑌𝑐 ∗
𝑌𝑐 2
𝑌 10 ∗ 𝑌𝑐 ∗ 2𝑐 𝐴𝑠 = 10 ∗ 𝑌𝑠 𝑌𝑐2 𝐴𝑠 = 0,50 ∗ (Ec. 2) 𝑌𝑠
C2.2 Cálculo de las Inercias: 𝑏 ∗ ℎ3 𝐼1 = + 𝐴 ∗ 𝑑2 12 10 ∗ 𝑌𝑐3 𝑌𝑐 2 𝐼1 = + 10 ∗ 𝑌𝑐 ∗ ( ) 12 2 𝐼1 =
10 10 ∗ 𝑌𝑐3 + ∗ 𝑌𝑐3 12 4
𝐼1 =
40 ∗ 𝑌𝑐3 12
𝐼1 = 3,33 ∗ 𝑌𝑐3
𝐼2 = 𝐼𝑣𝑎𝑟 + 𝐴𝑠 ∗ 𝑌𝑠2
𝐼 = 𝐼1 + 𝐼2 𝐼 = 3,33 ∗ 𝑌𝑐3 + 0,50 ∗
𝑌𝑐2 ∗ 𝑌𝑠2 𝑌𝑠
𝐼 = 3,33 ∗ 𝑌𝑐3 + 0,50 ∗ 𝑌𝑐2 ∗ 𝑌𝑠 𝐼 = 3,33 ∗ 𝑌𝑐3 + 0,50 ∗ 𝑌𝑐2 ∗ (25 − 𝑌𝑐 ) 𝐼 = 3,33 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 − 0,50 ∗ 𝑌𝑐3 𝐼 = 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 (𝐸𝑐. 3)
PARA LAS VIGUETAS LATERALES 𝑀𝑚á𝑥 = 9,563 𝐾𝑁 ∗ 𝑚 C2.3 Fórmula de la flexión: 𝜎𝑐𝑚á𝑥. = 𝐼=
𝑀𝑚á𝑥. ∗ 𝑌𝑐 𝐼
𝑀𝑚á𝑥. ∗ 𝑌𝑐 (𝐸𝑐. 4) 𝜎𝑐𝑚á𝑥.
Ecuación 1, 2 y 3 en 4: 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 =
100 𝑐𝑚 1𝑚 ∗𝑌 𝑐 𝑁 1 𝑚2 20𝐸𝑋𝑃 (6) 2 ∗ 𝑚 1002 𝑐𝑚2
9,563 𝐸𝑋𝑃 (3) 𝑁 ∗ 𝑚 ∗
2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 = 478,15 ∗ 𝑌𝑐 2,83 ∗ 𝑌𝑐2 + 12,50 ∗ 𝑌𝑐 − 478,15 = 0 𝑌𝑐 = 10,976 𝑐𝑚 ≈ 11,00 𝑐𝑚 𝑌𝑠 = (25,00 − 11,00)𝑐𝑚 = 14,00 𝑐𝑚
C2.4 Área de acero: 𝐴𝑠 = 0,50 ∗
𝑌𝑐2 𝑌𝑠
112 𝐴𝑠 = 0,50 ∗ 𝑐𝑚2 14 𝐴𝑠 = 4,321 𝑐𝑚2 ∴ 2∅18 𝑚𝑚 (5,09 𝑐𝑚2 )
PARA LA VIGUETA CENTRAL 𝑀𝑚á𝑥 = 6,75 𝐾𝑁 ∗ 𝑚 𝑌𝑐 + 𝑌𝑠 = 25,00 𝑐𝑚 (Ec. 1) 𝐴𝑠 = 0,50 ∗
𝑌𝑐2 (Ec. 2) 𝑌𝑠
𝐼 = 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 (𝐸𝑐. 3) 𝐼=
𝑀𝑚á𝑥. ∗ 𝑌𝑐 (𝐸𝑐. 4) 𝜎𝑐𝑚á𝑥.
Ecuación 1, 2 y 3 en 4: 100 𝑐𝑚 1𝑚 ∗𝑌 2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 = 𝑐 𝑁 1 𝑚2 20𝐸𝑋𝑃(6) 2 ∗ 𝑚 1002 𝑐𝑚2 6,75 𝐸𝑋𝑃 (3) 𝑁 ∗ 𝑚 ∗
2,83 ∗ 𝑌𝑐3 + 12,50 ∗ 𝑌𝑐2 = 337,50 ∗ 𝑌𝑐 2,83 ∗ 𝑌𝑐2 + 12,50 ∗ 𝑌𝑐 − 337,50 = 0 𝑌𝑐 = 8,933 𝑐𝑚 ≈ 9,00 𝑐𝑚 𝑌𝑠 = (25,00 − 9,00)𝑐𝑚 = 16,00 𝑐𝑚
C2.4 Área de acero: 𝑌𝑐2 𝐴𝑠 = 0,50 ∗ 𝑌𝑠 𝐴𝑠 = 0,50 ∗
92 𝑐𝑚2 16
𝐴𝑠 = 2,531 𝑐𝑚2 ∴ 2∅14 𝑚𝑚 (3,08 𝑐𝑚2 )
(d) Mostrar un esquema de la sección trasversal con la ubicación de las barras.
VIGUETA LATERAL
VIGUETA CENTRAL