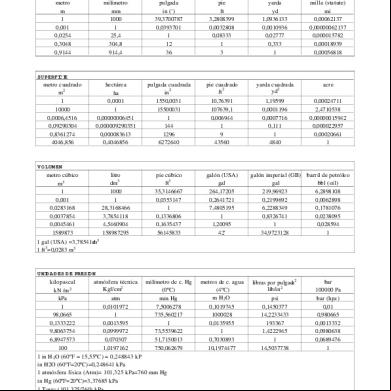
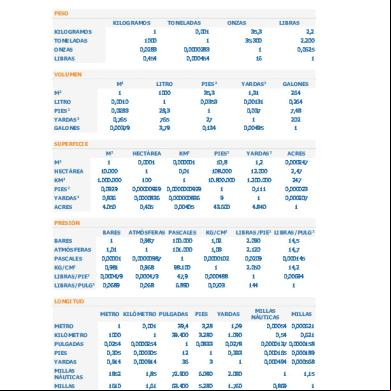
Conversion De Unidades 203x5e

UNIVERSIDAD NACIONAL DE HUANCAVELICA ESCUELA ACADEMICO PROFESIONAL DE INGENIERIA CIVIL

QUIMICA CONVERSION DE UNIDADDES Docente: Ing. Alfredo Grover Rojas Carrizales

©

2016

NASA

PARCS es una misión de reloj atómico programada para volar a la Estación Espacial Internacional (EEI) en 2008. La misión, 18-Jul.-18 por la NASA, implica un reloj atómico de cesio de láser costeada UNHmejorar - Ingeniería la Civilprecisión de la toma 2 de tiempo en la Tierra. frío para

Objetivos: Después de completar este módulo, deberá: • Mencionar y dar las unidades SI de las siete cantidades fundamentales. • Escribir las unidades base para masa, longitud y tiempo en unidades SI y USCU. • Convertir una unidad a otra para la misma cantidad cuando se dan definiciones necesarias. • Discutir y aplicar convenciones para dígitos significativos y precisión de mediciones. 18-Jul.-18

UNH - Ingeniería Civil

3

Cantidades físicas Una cantidad física es una propiedad cuantificable o asignable adscrita a un fenómeno, cuerpo o sustancia particular.

Longitud

Carga eléctrica

Tiempo

18-Jul.-18 UNH - Ingeniería Civil

4

Unidades de medición Una unidad es una cantidad física particular con la que se comparan otras cantidades del mismo tipo para expresar su valor. Un metro es una unidad establecida para medir longitud. Medición del diámetro del disco.

UNH - Ingeniería Civil

Con base en la definición, se dice que el diámetro es 0.12 m o 12 centímetros. 5

18-Jul.-18

Unidad SI de medición para longitud Un metro es la longitud de la ruta recorrida por una onda luminosa en el vacío en un intervalo de tiempo de 1/299,792,458 segundos.

1m t= 18-Jul.-18 UNH - Ingeniería Civil

1 segundo 299,792,458 6

Unidad SI de medición de masa El kilogramo es la unidad de masa – es igual a la masa del prototipo internacional del kilogramo. Este estándar es el único que requiere comparación para validar un artefacto. En la Oficina Internacional de Pesos y Medidas hay una copia del estándar. 18-Jul.-18 UNH - Ingeniería Civil

7

Unidad SI de medición de tiempo El segundo es la duración de 9 192 631 770 periodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado base del átomo de cesio 133. Reloj atómico de fuente de cesio: El tiempo primario y la frecuencia estándar para el USA (NIST) 18-Jul.-18 UNH - Ingeniería Civil

8

Siete unidades fundamentales Website: http://physics.nist.gov/cuu/index.html

Cantidad Longitud Masa Tiempo Corriente eléctrica Temperatura Intensidad luminosa Cantidad de 18-Jul.-18 sustancia UNH - Ingeniería Civil

Unidad

Símbolo

Metro Kilogramo Segundo Ampere Kelvin Candela Mol

m kg s a K cd mol

9

Sistemas de unidades Sistema SI: Sistema internacional de unidades establecido por el Comité Internacional de Pesos y Medidas. Dichas unidades se basan en definiciones estrictas y son las únicas unidades oficiales para cantidades físicas.

Unidades usuales en EUA (USCU): Unidades más antiguas todavía de uso común en Estados Unidos, pero las definiciones se deben basar en unidades SI. 18-Jul.-18

UNH - Ingeniería Civil

10

Unidades para mecánica En mecánica sólo se usan tres cantidades fundamentales: masa, longitud y tiempo. Una cantidad adicional, fuerza, se deriva de estas tres. Cantidad

Unidad SI

Unidad USCS

Masa

kilogramo (kg)

slug (slug)

Longitud

metro (m)

pie (ft)

Tiempo

segundo (s)

segundo (s)

Fuerza

newton (N)

libra (lb)

18-Jul.-18 UNH - Ingeniería Civil

11

Procedimiento para convertir unidades 1. Escriba la cantidad a convertir. 2. Defina cada unidad en términos de la unidad deseada. 3. Por cada definición, forme dos factores de conversión, uno como recíproco del otro.

4. Multiplique la cantidad a convertir por aquellos factores que cancelarán todo menos las unidades deseadas.

18-Jul.-18

UNH - Ingeniería Civil

12

Ejemplo 1: Convertir 12 in. a centímetros dado que 1 in. = 2.54 cm. Paso 1: Escriba la cantidad a convertir.

12 in.

Paso 2. Defina cada unidad en términos de la unidad deseada.

Paso 3. Para cada definición, forme dos factores de conversión, uno como el recíproco 18-Jul.-18 - Ingeniería Civil del UNH otro.

1 in. = 2.54 cm 1 in. 2.54 cm 2.54 cm 1 in 13

Ejemplo 1 (cont.): Convertir 12 in. a centímetros dado que 1 in. = 2.54 cm. Del paso 3.

1 in. 2.54 cm

o

2.54 cm 1 in

Paso 4. Multiplique por aquellos factores que cancelarán todo menos las unidades deseadas. Trate algebraicamente los símbolos de unidades. 2 1 in. in.   12 in.   = 4.72 cm  2.54 cm 

¡Mala elección!

¡Respuesta  2.54 cm  12 in.   = 30.5 cm correcta! 18-Jul.-18  1 in.  UNH - Ingeniería Civil

14

Ejemplo 2: Convertir 60 mi/h a unidades de km/s dado 1 mi. = 5280 ft y 1 h = 3600 s. Paso 1: Escriba la cantidad a convertir.

mi 60 h

Nota: Escriba las unidades de modo que los numeradores y denominadores de las fracciones sean claros. Paso 2. Defina cada unidad en términos de las unidades deseadas.

1 mi. = 5280 ft 18-Jul.-18 UNH - Ingeniería Civil

1 h = 360015s

Ej. 2 (cont): Convertir 60 mi/h a unidades de km/s dado que 1 mi. = 5280 ft y 1 h = 3600 s.

Paso 3. Para cada definición, forme dos factores de conversión, uno como recíproco del otro. 1 mi = 5280 ft 1 h = 3600 s

1 mi 5280 ft

5280 ft or 1 mi

1h 3600 s or 3600 s 1h

El paso 3, que se muestra aquí por claridad, en 18-Jul.-18 realidad se puede hacer mentalmente y no se UNH - Ingeniería Civil 16 necesita escribir.

Ej. 2 (cont.): Convertir 60 mi/h a unidades de ft/s dado que 1 mi. = 5280 ft y 1 h = 3600 s.

Paso 4. Elija factores para cancelar las unidades no deseadas.

mi  5280 ft  1 h  60    = 88.0 m/s h  1 mi  3600 s  Tratar algebraicamente la conversión de unidades ayuda a ver si una definición se usará como multiplicador 18-Jul.-18 oUNHcomo divisor. - Ingeniería Civil 17

Incertidumbre de medición Todas las mediciones se suponen aproximadas con el último dígito estimado.

0

1

Aquí, la longitud en “cm” se escribe como:

2

1.43 cm El último dígito “3” se estima como 0.3 del intervalo entre 3 y 4. 18-Jul.-18 UNH - Ingeniería Civil

18

Mediciones estimadas (cont.) Longitud = 1.43 cm

0

1

2

El último dígito es estimación, pero es significativo. Dice que la longitud real está entre 1.40 cm y 1.50 cm. Sin embargo, no sería posible estimar otro dígito, como 1.436. Esta medición de longitud se puede dar a tres dígitos significativos, con el último estimado. 18-Jul.-18 UNH - Ingeniería Civil

19

Dígitos significativos y números Cuando se escriben números, los ceros que se usan SÓLO para ayudar a ubicar el punto decimal NO son significativos, los otros sí. Vea los ejemplos.

0.0062 cm 4.0500 cm 0.1061 cm

2 cifras significativas 5 cifras significativas 4 cifras significativas

50.0 cm

3 cifras significativas

50,600 cm

3 cifras significativas

18-Jul.-18

UNH - Ingeniería Civil

20

Regla 1. Cuando se multiplican o dividen números aproximados, el número de dígitos significativos en la respuesta final es el mismo que el número de dígitos significativos en el menos preciso de los factores. 45 N = 6.97015 N/m2 Ejemplo: P = (3.22 m)(2.005 m)

El factor menos significativo (45) sólo tiene dos (2) dígitos, así que sólo se justifican dos en la respuesta.

La forma correcta de 18-Jul.-18 escribir la respuesta es: UNH - Ingeniería Civil

P = 7.0 N/m2 21

Regla 2. Cuando se suman o restan números aproximados, el número de dígitos significativos será igual al número más pequeño de lugares decimales de cualquier término en la suma o diferencia.

Ej: 9.65 cm + 8.4 cm – 2.89 cm = 15.16 cm Note que la medición menos precisa es 8.4 cm. Por tanto, la respuesta debe estar a la décima de cm más cercana aun cuando requiera 3 dígitos significativos.

La forma correcta de 18-Jul.-18 escribir la respuesta es: UNH - Ingeniería Civil

15.2 cm 22

Ejemplo 3. Encuentre el área de una placa metálica que mide 95.7 cm por 32 cm. A = LW = (8.71 cm)(3.2 cm) = 27.872 cm2 Sólo 2 dígitos justificados:

A = 28 cm2

Ejemplo 4. Encuentre el perímetro de la placa que mide 95.7 cm de largo y 32 cm de ancho.

p = 8.71 cm + 3.2 cm + 8.71 cm + 3.2 cm Respuesta a décimas de cm: UNH - Ingeniería Civil

p = 23.8 cm

18-Jul.-18

23

Redondeo de números Recuerde que las cifras significativas se aplican al resultado que reporte. Redondear sus números en el proceso puede conducir a errores.

Regla: Siempre retenga en sus cálculos al menos una cifra significativa más que el número que debe reportar en el resultado. Con las calculadoras, usualmente es más fácil 18-Jul.-18conservar todos los dígitos hasta que UNH - Ingeniería Civil 24 reporte el resultado.

Reglas para redondeo de números Regla 1. Si el resto más allá del último dígito a reportar es menor que 5, elimine el último dígito.

Regla 2. Si el resto es mayor que 5, aumente el dígito final por 1. Regla 3. Para evitar sesgos de redondeo, si el resto es exactamente 5, entonces redondee el último dígito al número par más cercano. 18-Jul.-18 UNH - Ingeniería Civil

25

Ejemplos Regla 1. Si el resto más allá del último dígito a reportar es menor que 5, elimine el último dígito. Redondee lo siguiente a 3 cifras significativas:

18-Jul.-18

4.99499

se vuelve

4.99

0.09403

se vuelve

0.0940

95,632

se vuelve

95,600

0.02032

se vuelve

0.0203

UNH - Ingeniería Civil

26

Ejemplos Regla 2. Si el resto es mayor que 5, aumente el dígito final por 1. Redondee lo siguiente a 3 cifras significativas:

18-Jul.-18

2.3452

se vuelve

2.35

0.08757

se vuelve

0.0876

23,650.01

se vuelve

23,700

4.99502

se vuelve

5.00

UNH - Ingeniería Civil

27

Ejemplos Regla 3. Para evitar sesgos de redondeo, si el resto es exactamente 5, entonces redondee el último dígito al número par más cercano. Redondee lo siguiente a 3 cifras significativas: 3.77500

se vuelve

3.78

0.024450

se vuelve

0.0244

96,6500

se vuelve

96,600

5.09500 UNH - Ingeniería Civil

se vuelve28

5.10

18-Jul.-18

Trabajar con números El trabajo en clase y el de laboratorio se deben tratar de modo diferente. En clase, por lo general no se conocen las incertidumbres en las cantidades. Redondee a 3 cifras significativas en la mayoría de 18-Jul.-18 los casos. UNH - Ingeniería Civil

En laboratorio, se conocen las limitaciones de las mediciones. No se deben conservar dígitos que no estén justificados. 29

Ejemplo para salón de clase: Un auto que inicialmente viaja a 46 m/s experimenta aceleración constante de 2 m/s2 durante un tiempo de 4.3 s. Encuentre el desplazamiento total dada la fórmula.

x = v0t  at 1 2

2

= (46 m/s)(4.3 s)  12 (2 m/s 2 )(4.3 s) 2 = 197.8 m + 18.48 m = 216.29 m Para el trabajo en clase, suponga que toda la información dada es precisa a 3 cifras significativas. 18-Jul.-18 UNH - Ingeniería Civil

x = 217 m 30

Ejemplo de laboratorio: Una hoja metálica mide 233.3 mm de largo y 9.3 mm de ancho. Encuentre su área. Note que la precisión de cada medida está a la décima de milímetro más cercana. Sin embargo, la longitud tiene 4 dígitos significativos y el ancho sólo 2. ¿Cuántos dígitos significativos hay en el producto de longitud y ancho (área)? Dos (9.3 tiene menos dígitos significativos). 18-Jul.-18 UNH - Ingeniería Civil

31

Ejemplo para laboratorio (cont.): Una hoja metálica mide 233.3 mm de largo y 9.3 mm de ancho. Encuentre su área. Área = LA = (233.3 mm)(9.3 mm) Área = 2169.69 mm2

A = 9.3 mm

Pero sólo se pueden tener dos dígitos significativos. Por ende, la respuesta se convierte en: 18-Jul.-18

L = 233.3 mm

Área = 2200 mm2

UNH - Ingeniería Civil

32

Ejemplo para laboratorio (cont.): Encuentre el perímetro de la hoja metálica que mide L = 233.3 mm y A = 9.3 mm. (Regla de la suma)

p = 233.3 mm + 9.3 mm + 233.3 mm + 9.3 mm p = 485.2 mm

A = 9.3 mm

Note: The answer Nota: En este caso, is el determined by más the resultado tiene least precise measure. dígitos significativos que factorofancho. (theeltenth a mm) 18-Jul.-18

L = 233.3 mm

Perímetro = 485.2 mm

UNH - Ingeniería Civil

33

Notación científica La notación científica proporciona un método abreviado para expresar números o muy pequeños o muy grandes.

Ejemplos:

-9 = 0.000000001 10 -6 = 0.000001 10

93,000,000 mi = 9.30 x 107 mi

-3 = 0.001 10

0.00457 m = 4.57 x 10-3 m

1 = 100 1000 = 103 1,000,000 = 106 1,000,000,000 = 109

876 m 8.76 x 102 m v= = 0.00370 s 3.70 x 10-3s

v = 3.24 x 10 m/s 5

18-Jul.-18

UNH - Ingeniería Civil

34

Notación científica y cifras significativas Con la notación científica uno puede fácilmente seguir la pista de los dígitos significativos al usar sólo aquellos dígitos necesarios en la mantisa y dejar que la potencia de diez ubique el decimal.

Ejemplo. Exprese el número 0.0006798 m, preciso a tres dígitos significativos. 6.80 x 10-4 m

Mantisa x 10-4 m

El18-Jul.-18 “0” es significativo, el último dígito en duda. UNH - Ingeniería Civil

35

RESUMEN

Siete unidades fundamentales Cantidad

Unidad

Símbolo

Longitud Masa Tiempo Corriente eléctrica Temperatura Intensidad luminosa Cantidad de sustancia

Metro Kilogramo Segundo Ampere Kelvin Candela Mol

m kg s a K cd mol

18-Jul.-18

UNH - Ingeniería Civil

36

Resumen: Procedimiento para convertir unidades 1. Escriba la cantidad a convertir. 2. Defina cada unidad en términos de la unidad deseada. 3. Para cada definición, forme dos factores de conversión, uno como el recíproco del otro.

4. Multiplique la cantidad a convertir por aquellos factores que cancelarán todo menos las unidades deseadas. 18-Jul.-18 UNH - Ingeniería Civil

37

Resumen –Dígitos significativos Regla 1. Cuando se multipliquen o dividan números aproximados, el número de dígitos significativos en la respuesta final es igual al número de dígitos significativos en el menos preciso de los factores. Regla 2. Cuando se sumen o resten números aproximados, el número de dígitos significativos debe ser igual al número más pequeño de lugares decimales de cualquier término en la 18-Jul.-18 sumaUNHo- Ingeniería diferencia. Civil 38

Reglas para redondeo de números Regla 1. Si el resto más allá del último dígito a

reportar es menor que 5, elimine el último dígito.

Regla 2. Si el resto es mayor que 5, aumente el dígito final por 1. Regla 3. Para evitar sesgos de redondeo, si el resto es exactamente 5, entonces redondee el último dígito al número par más cercano. 18-Jul.-18 UNH - Ingeniería Civil

39

Trabajo con números El trabajo en el salón y en el laboratorio se deben tratar de modo diferente a menos que se diga lo contrario.

En el laboratorio, el En el salón, se supone número de cifras que toda la información significativas dependerá 18-Jul.-18 dada es precisa a 3 de 40las limitaciones de los UNH - Ingeniería Civil cifras significativas.

Conclusión del módulo de dígitos significativos en las mediciones

UNH - Ingeniería Civil

41

18-Jul.-18