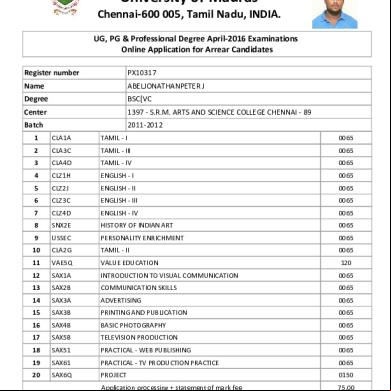
Projection Of Planes 1646y
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3b7i
Overview 3e4r5l
& View Projection Of Planes as PDF for free.
More details w3441
- Words: 3,381
- Pages: 22
3 Projections of Planes BASICS A plane is a two dimensional object having length and breadth only. Its thickness is always neglected. Various shapes of plane figures are considered such as square, rectangle, circle, pentagon, hexagon, etc.
(i)
(v)
(ii)
(iii)
(vi)
(iv)
(vii)
Figure 3.1
There are two types of planes 1. Perpendicular planes which have their surface perpendicular to any one of the reference planes and parallel or inclined to the other reference plane. 2. Oblique planes which have their surface inclined to both the reference planes.
74
Lesson Plan for Engineering Graphics
Traces of a Plane The trace of a plane is the line of intersection or meeting of the plane surface with the reference plane; if necessary the plane surface is extended to intersect the reference plane. The intersection line of the plane surface with HP is called the Horizontal Trace (HT) and that of VP is called the Vertical Trace (VT).
POSITIONS OF A PLANE A plane figure is positioned with reference to the reference planes by referring its surface in the following possible positions. 1. Surface of the plane kept perpendicular to HP and parallel to VP 2. Surface of the plane kept perpendicular to VP and parallel to HP 3. Surface of the plane kept perpendicular to both HP and VP 4. Surface of the plane kept inclined to HP and perpendicular to VP 5. Surface of the plane kept inclined to VP and perpendicular to HP 6. Surface of the plane kept inclined to both HP and VP
Projections of a Plane with its Surface Perpendicular to HP and Parallel to VP Consider a square plane ABCD having its surface perpendicular to HP and parallel to VP as in Fig. 3.2(i).
(i)
(ii) Figure 3.2
75
Projections of Planes
The front view is projected onto VP which is a square a1,b1,c1,d1 having true shape and size. The top view is projected onto HP and is a line ab(c)(d) parallel to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet HP to get the HT which coincides with the top view of the plane. It does not have a VT because the plane is parallel to VP. The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.2(ii).
Projections of a Plane with its Surface Perpendicular to VP and Parallel to HP Consider a square plane ABCD with its surface perpendicular to VP and parallel to HP as in Fig. 3.3(i).
(i)
(ii) Figure 3.3
The top view is projected onto HP which is a square abcd having true shape and size. The front view is projected onto VP and is a line a¢b¢(c¢)(d¢) parallel to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet VP to get the VT which coincides with the front view of the plane. It does not have a HT because the plane is parallel to HP. The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.3(ii).
76
Lesson Plan for Engineering Graphics
Projections of a Plane with its Surface Perpendicular to both HP and VP Consider a square plane ABCD having its surface perpendicular to both HP and VP as in Fig. 3.4(i). The front view b¢c¢(d¢)(a¢) and top view ab(c)(d) are projected onto VP and HP respectively. Both the views are lines perpendicular to the XY line. The true shape of the plane is obtained in the side view which is projected onto a profile plane (PP) which is perpendicular to both HP and VP. In this case, the left side view a≤b≤c≤d≤ is obtained on the PP which is at the right side of the given object (plane). The plane surface is extended to meet HP and VP to get HT and VT which coincide with the top and front views respectively. The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.4(ii).
(i)
(ii) Figure 3.4
Projections of a Plane with its Surface Inclined to HP and Perpendicular to VP Consider a square plane ABCD with its surface inclined at an angle q to HP and perpendicular to VP as in Fig. 3.5(i).
77
Projections of Planes
The top view abcd is projected onto HP. It is smaller than the true shape and size. The front view is projected onto VP and is a line a¢b¢(c¢)(d¢) inclined at an angle q to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet HP to get the HT which is a line perpendicular to XY. The plane surface is also extended to meet VP to get the VT which is a line inclined at an angle q to XY. The projections and traces obtained are drawn with references to the XY line as shown in Fig. 3.5(ii).
(i)
(ii) Figure 3.5
Projections of a Plane with its Surface Inclined to VP and Perpendicular to HP Consider a square plane ABCD with its surface inclined at an angle f to VP and perpendicular to HP as shown in Fig. 3.6(i). The front view a¢b¢c¢d¢ is projected onto VP. It is smaller than the true shape and size. The top view is projected onto HP and is a line ab(c)(d) inclined at an angle f to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet VP to get the VT which is a line perpendicular to XY. The plane surface is also extended to meet HP to get the HT which is a line inclined at an angle f to XY.
78
Lesson Plan for Engineering Graphics
The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.6(ii).
(i)
(ii) Figure 3.6
Note: (i) When a plane is placed with its surface inclined to one plane and perpendicular to the other plane, its projections cannot be drawn directly. It is obtained in two steps and will be discussed in the examples that follow. (ii) When a plane is placed with its surface inclined to both the reference planes, its projections are obtained in three steps which will be discussed in the following examples.
79
Projections of Planes
Space for Rough Work
80
Lesson Plan for Engineering Graphics
81
Projections of Planes
PRACTICE PROBLEMS Problem 1 A pentagonal plate of side 35mm is placed with its surface vertical and parallel to VP. Draw its projections when one of the sides is perpendicular to HP. Solution When a plane is placed with its surface parallel to VP and perpendicular to HP, draw its front view which will have the true shape and size. Project the top view which will be a line parallel to XY. To draw the projections 1. Draw a line perpendicular to XY. Arbitrarily mark the side 35 mm of the pentagon on this line and construct the pentagon. Name the corners as a¢b¢c¢d¢e¢. 2. Project the top view of the plane by projecting all the corners from the front view which is a line a(b)e(c)d drawn parallel to the XY line.
Problem 2 An equilateral triangular plate of side 50mm is kept with its plane parallel to HP and one of the sides of the plate inclined at 45° to VP. Draw its projections. Solution When a plane is placed with its surface parallel to HP and perpendicular to VP, draw its top view which will have the true shape and size. Project the front view which will be a line parallel to XY. To draw the projections 1. Draw a line inclined at 45° to XY. Arbitrarily mark the side 50mm of the triangular plate on this line and construct the triangle. Name the corners as a,b and c in top view . 2. Project the front view a¢(c¢)b¢ of the plane by projecting the top view which is a line drawn parallel to XY line.
82
Lesson Plan for Engineering Graphics
Projections of Planes
83
Problem 3 A regular hexagonal plate of side 30 mm has its surface perpendicular to both HP and VP. Draw its projections when two of the sides are parallel to HP. Solution When a plane is placed with its surface perpendicular to both HP and VP, draw its side view which will have the true shape and size. Project the top and front views which are lines perpendicular to XY. To draw the projections 1. Draw a line parallel to XY in the side view. Arbitrarily mark the side 30 mm of the hexagon on this line and construct the hexagon in the left side view. Name the corners as a≤b≤c≤d≤, etc. 2. Project the top view of the plane by projecting all the corners from the side view. From a≤ draw a perpendicular line to meet XY, from this point draw a line at 45° to XY to meet x1y1 and a line parallel to XY. Mark the top view a arbitrarily on this line. Similarly the other corners b≤,c≤ and d≤ are projected to get the top view a(b)(c)def as a line perpendicular to XY. 3. Project the front view a¢ by drawing a vertical line from top view a and a horizontal line from a≤ to get the intersection point a¢. Similarly draw vertical lines from b, c, d, e and f. Draw horizontal lines from b≤, c≤, d≤, e≤ and f ≤ to get the front view b¢, c¢, d¢, e¢ and f¢ perpendicular to XY.
84
Lesson Plan for Engineering Graphics
Projections of Planes
85
Problem 4 A circular plate of negligible thickness and 60mm diameter appears as an ellipse in the top view, having its major axis 60mm and minor axis 30mm. Draw its projections and find the inclination of the plate with HP. Solution When a plane is placed with its surface inclined to HP and perpendicular to VP, its projections are obtained in two steps. Step 1: Assume that the plane has its surface parallel to HP and perpendicular to VP. Draw its top view which will have the true shape and size. Project the front view which will be a line parallel to XY. Step 2: Reproduce the front view tilted to the given angle q to HP and project the top view of the plane which will be smaller than the true shape and size. To draw the projections 1. Assume that the plate has its surface parallel to HP and perpendicular to VP. Draw its top view—it is a circle of radius 30 mm. 2. Project and get the front view which is a line on XY. 3. As the circle does not have any corners, divide the circle into equal parts, say 8, (students are asked to divide the circle into a minimum of 12 parts) in such a way that 8 points are marked on its circumference and project them to the front view. 4. Draw the end projectors in front view as 30mm (minor axis of ellipse) and reproduce the front view by drawing an arc to cut the end projector, in such a way that the end a¢ is on XY line.The angle made by the reproduced front view with XY is the inclination of the plane with HP (q). 5. Draw horizontal lines from a, b, c, etc., and vertical lines from a¢1, b¢1, c¢1, etc., to get the required top view a1, b1, c1, etc. 6. a1, b1, c1, etc., by drawing a smooth curve to get the top view of the circle as an ellipse having minor axis 30mm and major axis 60mm.
86
Lesson Plan for Engineering Graphics
Projections of Planes
87
Problem 5 Draw the projection of a circular lamina which has 50mm as diameter and its plane vertical and inclined at 45° to the VP. Its centre is 40mm above HP and 60mm infront of VP. Solution When a plane is placed with its surface inclined to VP and perpendicular to HP, its projections are obtained in two steps. Step 1: Assume that the plane has its surface parallel to VP and perpendicular to HP. Draw its front view which will have the true shape and size. Project the top view which will be a line parallel to XY. Step 2: Reproduce the top view tilted to the given angle f to VP and project the front view of the plane which will be smaller than the true shape and size. To draw the projections 1. Draw the front view of the circle considering the centre 40mm above XY line and radius 25mm. 2. As the circle does not have any corners, divide the circle into equal parts, say 8, (students are asked to divide the circle into a minimum of 12 parts) in such a way that 8 points are marked on its circumference and project them to the front view. 3. Project the top view of the plane by projecting the front view a¢b¢c¢ etc to get the top view a(b)(c)(d)efgh as a line on XY line. 4. Tilt and reproduce the top view a(b)(c)(d)efgh to the required angle 45° with XY in such a way that the centre (c1)g1 is 60 mm from the XY line. 5. Draw horizontal lines from a1b1c1, etc., and vertical lines from top view a1, b1, c1, etc., to get the required front view a¢1b¢1c¢1, etc. 6. a¢1b¢1c¢1, to get the front view of the circular plate which is an ellipse.
88
Lesson Plan for Engineering Graphics
Projections of Planes
89
Problem 6 A regular hexagon of side 35 mm has a corner in the HP. Its surface is inclined at 45º to HP. The top view of the diagnol through the corner in HP makes an angle of 60º with VP. Draw its projections. Solution In this position, the surface of the plate is inclined to both HP and VP, its projections are obtained in three steps. Step 1: Assume that the plane has its surface parallel to HP and perpendicular to VP. Draw its top view which will have the true shape and size. Project the front view which will be a line parallel to the XY line. Step 2: Reproduce the front view tilted to the given angle q to HP and project the top view of the plane which will be smaller than the true shape and size. Step 3: Reproduce the top view by considering the side/diagonal of the plate that makes, the given angle with VP. Project the front view of the plane which is also smaller than the true shape and size. To draw the projections 1. Draw the top view of the hexagon considering that one of the sides is parallel to XY. Then only while tilting the surface to the required angle with HP, a corner of the plane will rest on HP. 2. The front view of the plane is projected and obtained on XY as a line a¢b¢(f ¢)(e¢)c¢d¢ 3. Tilt and reproduce the front view a¢b¢(f ¢)(e¢)c¢d to the given angle 45° with XY in such a way that the end a¢ is on XY line. 4. Draw horizontal lines from top view a, b, c, etc., and vertical lines from front view a¢1, b¢1, c¢1, etc., to get the top view a1,b1c1d1, etc., smaller than the true shape and size. 5. Reproduce the top view a1, b1, c1, d1, e1, f1 in such a way that the diagonal a1d1 is inclined to the given angle 60° to VP. 6. Draw horizontal lines from a¢1, b¢1, c¢1, etc., and vertical lines from top view a2, b2, c2, etc., to get the required front view a¢2, b¢2, c¢2, d¢2, e¢2, f ¢2 of the plate smaller than the true shape and size.
90
Lesson Plan for Engineering Graphics
Projections of Planes
91
Problem 7 Draw the projections of a regular pentagon of side 40 mm which has its surface inclined at 30∞ to VP and a side parallel to VP and inclined at 60∞ to HP. Solution In this position, the surface of the plate is inclined to both VP and HP. Its projections are obtained in three steps. Step 1: Assume that the plate has its surface parallel to VP and perpendicular to HP. Draw its front view which will have the true shape and size. Project the top view which will be a line parallel to XY line. Step 2: Reproduce the top view tilted to the given angle f to VP and project the front view of the plane which will be smaller than the true shape and size. Step 3: Reproduce the front view by considering the side of the plate that makes the given angle with HP. Project the top view of the plane which is also smaller than the true shape and size. To draw the projections 1. Draw the front view of the pentagon considering one of the sides perpendicular to XY. Then only while tilting the surface to the required angle with VP, this side of the plane will rest on VP. 2. The top view of the plane is projected and obtained on XY as a line. 3. Tilt and reproduce the top view line to the given angle 30° with XY in such a way that the end a(b) is on the XY line. 4. Draw horizontal lines from front view a, b c, etc and vertical lines from top view a1, b1, c1, etc., to get the front view of the plane which is smaller than the true shape and size. 5. Reproduce the front view in such a way that the side a¢1b¢1 is inclined to the given angle 60° to HP. 6. Draw horizontal lines from a¢1, b¢1, c¢1, etc., and vertical lines from a¢2, b¢2, c¢2, etc., to get the required top view of the pentagon plate which is smaller than the true shape and size.
92
Lesson Plan for Engineering Graphics
Projections of Planes
93
Problem 8 Draw the projections of a regular hexagon of side 25 mm, having one of its sides on the ground and inclined at 60∞ to VP and its surface making an angle of 45∞ with the ground. Solution In this position, the surface of the plate is inclined to both HP and VP, its projections are obtained in three steps. Step 1: Assume that the plane has its surface parallel to HP and perpendicular to VP. Draw its top view which will have the true shape and size. Project the front view which will be a line parallel to the XY line. Step 2: Reproduce the front view tilted to the given angle q to HP and project the top view of the plane which will be smaller than the true shape and size. Step 3: Reproduce the top view by considering the side of the plate that makes, the given angle with VP. Project the front view of the plane which is also smaller than the true shape and size. To draw the projections 1. Draw the top view of the hexagon considering one of the sides is perpendicular to XY. Then only while tilting the surface to the required angle with HP, this side of the plane will rest on HP. 2. The front view of the plane is projected and obtained on XY as a line (a)¢b¢(f ¢)c¢(e¢)d¢. 3. Tilt and reproduce the front view (a¢)b¢(f ¢)c¢(e¢)d¢ to the given angle 45° with XY in such a way that the end (a¢)b¢ is on XY line. 4. Draw horizontal lines from top view a, b, c etc and vertical lines from front view a¢1, b¢1, c¢1, etc., to get the top view a¢1,b¢1,c¢1,d¢1,e¢1,f ¢1, smaller than the true shape and size. 5. Reproduce the top view a1, b1, c1, d1, e1, f1, in such a way that the side a1, b1 is inclined to the given angle 30° to VP. 6. Draw horizontal lines from a¢1, b¢1, c¢1 etc and vertical lines from top view a1, b1, c1, etc., to get the required front view a¢2,b¢2,c¢2,d¢2,e¢2,f ¢2 of the plate smaller than the true shape and size.
94
Lesson Plan for Engineering Graphics
Space for Rough Work
(i)
(v)
(ii)
(iii)
(vi)
(iv)
(vii)
Figure 3.1
There are two types of planes 1. Perpendicular planes which have their surface perpendicular to any one of the reference planes and parallel or inclined to the other reference plane. 2. Oblique planes which have their surface inclined to both the reference planes.
74
Lesson Plan for Engineering Graphics
Traces of a Plane The trace of a plane is the line of intersection or meeting of the plane surface with the reference plane; if necessary the plane surface is extended to intersect the reference plane. The intersection line of the plane surface with HP is called the Horizontal Trace (HT) and that of VP is called the Vertical Trace (VT).
POSITIONS OF A PLANE A plane figure is positioned with reference to the reference planes by referring its surface in the following possible positions. 1. Surface of the plane kept perpendicular to HP and parallel to VP 2. Surface of the plane kept perpendicular to VP and parallel to HP 3. Surface of the plane kept perpendicular to both HP and VP 4. Surface of the plane kept inclined to HP and perpendicular to VP 5. Surface of the plane kept inclined to VP and perpendicular to HP 6. Surface of the plane kept inclined to both HP and VP
Projections of a Plane with its Surface Perpendicular to HP and Parallel to VP Consider a square plane ABCD having its surface perpendicular to HP and parallel to VP as in Fig. 3.2(i).
(i)
(ii) Figure 3.2
75
Projections of Planes
The front view is projected onto VP which is a square a1,b1,c1,d1 having true shape and size. The top view is projected onto HP and is a line ab(c)(d) parallel to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet HP to get the HT which coincides with the top view of the plane. It does not have a VT because the plane is parallel to VP. The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.2(ii).
Projections of a Plane with its Surface Perpendicular to VP and Parallel to HP Consider a square plane ABCD with its surface perpendicular to VP and parallel to HP as in Fig. 3.3(i).
(i)
(ii) Figure 3.3
The top view is projected onto HP which is a square abcd having true shape and size. The front view is projected onto VP and is a line a¢b¢(c¢)(d¢) parallel to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet VP to get the VT which coincides with the front view of the plane. It does not have a HT because the plane is parallel to HP. The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.3(ii).
76
Lesson Plan for Engineering Graphics
Projections of a Plane with its Surface Perpendicular to both HP and VP Consider a square plane ABCD having its surface perpendicular to both HP and VP as in Fig. 3.4(i). The front view b¢c¢(d¢)(a¢) and top view ab(c)(d) are projected onto VP and HP respectively. Both the views are lines perpendicular to the XY line. The true shape of the plane is obtained in the side view which is projected onto a profile plane (PP) which is perpendicular to both HP and VP. In this case, the left side view a≤b≤c≤d≤ is obtained on the PP which is at the right side of the given object (plane). The plane surface is extended to meet HP and VP to get HT and VT which coincide with the top and front views respectively. The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.4(ii).
(i)
(ii) Figure 3.4
Projections of a Plane with its Surface Inclined to HP and Perpendicular to VP Consider a square plane ABCD with its surface inclined at an angle q to HP and perpendicular to VP as in Fig. 3.5(i).
77
Projections of Planes
The top view abcd is projected onto HP. It is smaller than the true shape and size. The front view is projected onto VP and is a line a¢b¢(c¢)(d¢) inclined at an angle q to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet HP to get the HT which is a line perpendicular to XY. The plane surface is also extended to meet VP to get the VT which is a line inclined at an angle q to XY. The projections and traces obtained are drawn with references to the XY line as shown in Fig. 3.5(ii).
(i)
(ii) Figure 3.5
Projections of a Plane with its Surface Inclined to VP and Perpendicular to HP Consider a square plane ABCD with its surface inclined at an angle f to VP and perpendicular to HP as shown in Fig. 3.6(i). The front view a¢b¢c¢d¢ is projected onto VP. It is smaller than the true shape and size. The top view is projected onto HP and is a line ab(c)(d) inclined at an angle f to XY. The invisible corners are enclosed in ( ). The plane surface is extended to meet VP to get the VT which is a line perpendicular to XY. The plane surface is also extended to meet HP to get the HT which is a line inclined at an angle f to XY.
78
Lesson Plan for Engineering Graphics
The projections and traces obtained are drawn with reference to the XY line as shown in Fig. 3.6(ii).
(i)
(ii) Figure 3.6
Note: (i) When a plane is placed with its surface inclined to one plane and perpendicular to the other plane, its projections cannot be drawn directly. It is obtained in two steps and will be discussed in the examples that follow. (ii) When a plane is placed with its surface inclined to both the reference planes, its projections are obtained in three steps which will be discussed in the following examples.
79
Projections of Planes
Space for Rough Work
80
Lesson Plan for Engineering Graphics
81
Projections of Planes
PRACTICE PROBLEMS Problem 1 A pentagonal plate of side 35mm is placed with its surface vertical and parallel to VP. Draw its projections when one of the sides is perpendicular to HP. Solution When a plane is placed with its surface parallel to VP and perpendicular to HP, draw its front view which will have the true shape and size. Project the top view which will be a line parallel to XY. To draw the projections 1. Draw a line perpendicular to XY. Arbitrarily mark the side 35 mm of the pentagon on this line and construct the pentagon. Name the corners as a¢b¢c¢d¢e¢. 2. Project the top view of the plane by projecting all the corners from the front view which is a line a(b)e(c)d drawn parallel to the XY line.
Problem 2 An equilateral triangular plate of side 50mm is kept with its plane parallel to HP and one of the sides of the plate inclined at 45° to VP. Draw its projections. Solution When a plane is placed with its surface parallel to HP and perpendicular to VP, draw its top view which will have the true shape and size. Project the front view which will be a line parallel to XY. To draw the projections 1. Draw a line inclined at 45° to XY. Arbitrarily mark the side 50mm of the triangular plate on this line and construct the triangle. Name the corners as a,b and c in top view . 2. Project the front view a¢(c¢)b¢ of the plane by projecting the top view which is a line drawn parallel to XY line.
82
Lesson Plan for Engineering Graphics
Projections of Planes
83
Problem 3 A regular hexagonal plate of side 30 mm has its surface perpendicular to both HP and VP. Draw its projections when two of the sides are parallel to HP. Solution When a plane is placed with its surface perpendicular to both HP and VP, draw its side view which will have the true shape and size. Project the top and front views which are lines perpendicular to XY. To draw the projections 1. Draw a line parallel to XY in the side view. Arbitrarily mark the side 30 mm of the hexagon on this line and construct the hexagon in the left side view. Name the corners as a≤b≤c≤d≤, etc. 2. Project the top view of the plane by projecting all the corners from the side view. From a≤ draw a perpendicular line to meet XY, from this point draw a line at 45° to XY to meet x1y1 and a line parallel to XY. Mark the top view a arbitrarily on this line. Similarly the other corners b≤,c≤ and d≤ are projected to get the top view a(b)(c)def as a line perpendicular to XY. 3. Project the front view a¢ by drawing a vertical line from top view a and a horizontal line from a≤ to get the intersection point a¢. Similarly draw vertical lines from b, c, d, e and f. Draw horizontal lines from b≤, c≤, d≤, e≤ and f ≤ to get the front view b¢, c¢, d¢, e¢ and f¢ perpendicular to XY.
84
Lesson Plan for Engineering Graphics
Projections of Planes
85
Problem 4 A circular plate of negligible thickness and 60mm diameter appears as an ellipse in the top view, having its major axis 60mm and minor axis 30mm. Draw its projections and find the inclination of the plate with HP. Solution When a plane is placed with its surface inclined to HP and perpendicular to VP, its projections are obtained in two steps. Step 1: Assume that the plane has its surface parallel to HP and perpendicular to VP. Draw its top view which will have the true shape and size. Project the front view which will be a line parallel to XY. Step 2: Reproduce the front view tilted to the given angle q to HP and project the top view of the plane which will be smaller than the true shape and size. To draw the projections 1. Assume that the plate has its surface parallel to HP and perpendicular to VP. Draw its top view—it is a circle of radius 30 mm. 2. Project and get the front view which is a line on XY. 3. As the circle does not have any corners, divide the circle into equal parts, say 8, (students are asked to divide the circle into a minimum of 12 parts) in such a way that 8 points are marked on its circumference and project them to the front view. 4. Draw the end projectors in front view as 30mm (minor axis of ellipse) and reproduce the front view by drawing an arc to cut the end projector, in such a way that the end a¢ is on XY line.The angle made by the reproduced front view with XY is the inclination of the plane with HP (q). 5. Draw horizontal lines from a, b, c, etc., and vertical lines from a¢1, b¢1, c¢1, etc., to get the required top view a1, b1, c1, etc. 6. a1, b1, c1, etc., by drawing a smooth curve to get the top view of the circle as an ellipse having minor axis 30mm and major axis 60mm.
86
Lesson Plan for Engineering Graphics
Projections of Planes
87
Problem 5 Draw the projection of a circular lamina which has 50mm as diameter and its plane vertical and inclined at 45° to the VP. Its centre is 40mm above HP and 60mm infront of VP. Solution When a plane is placed with its surface inclined to VP and perpendicular to HP, its projections are obtained in two steps. Step 1: Assume that the plane has its surface parallel to VP and perpendicular to HP. Draw its front view which will have the true shape and size. Project the top view which will be a line parallel to XY. Step 2: Reproduce the top view tilted to the given angle f to VP and project the front view of the plane which will be smaller than the true shape and size. To draw the projections 1. Draw the front view of the circle considering the centre 40mm above XY line and radius 25mm. 2. As the circle does not have any corners, divide the circle into equal parts, say 8, (students are asked to divide the circle into a minimum of 12 parts) in such a way that 8 points are marked on its circumference and project them to the front view. 3. Project the top view of the plane by projecting the front view a¢b¢c¢ etc to get the top view a(b)(c)(d)efgh as a line on XY line. 4. Tilt and reproduce the top view a(b)(c)(d)efgh to the required angle 45° with XY in such a way that the centre (c1)g1 is 60 mm from the XY line. 5. Draw horizontal lines from a1b1c1, etc., and vertical lines from top view a1, b1, c1, etc., to get the required front view a¢1b¢1c¢1, etc. 6. a¢1b¢1c¢1, to get the front view of the circular plate which is an ellipse.
88
Lesson Plan for Engineering Graphics
Projections of Planes
89
Problem 6 A regular hexagon of side 35 mm has a corner in the HP. Its surface is inclined at 45º to HP. The top view of the diagnol through the corner in HP makes an angle of 60º with VP. Draw its projections. Solution In this position, the surface of the plate is inclined to both HP and VP, its projections are obtained in three steps. Step 1: Assume that the plane has its surface parallel to HP and perpendicular to VP. Draw its top view which will have the true shape and size. Project the front view which will be a line parallel to the XY line. Step 2: Reproduce the front view tilted to the given angle q to HP and project the top view of the plane which will be smaller than the true shape and size. Step 3: Reproduce the top view by considering the side/diagonal of the plate that makes, the given angle with VP. Project the front view of the plane which is also smaller than the true shape and size. To draw the projections 1. Draw the top view of the hexagon considering that one of the sides is parallel to XY. Then only while tilting the surface to the required angle with HP, a corner of the plane will rest on HP. 2. The front view of the plane is projected and obtained on XY as a line a¢b¢(f ¢)(e¢)c¢d¢ 3. Tilt and reproduce the front view a¢b¢(f ¢)(e¢)c¢d to the given angle 45° with XY in such a way that the end a¢ is on XY line. 4. Draw horizontal lines from top view a, b, c, etc., and vertical lines from front view a¢1, b¢1, c¢1, etc., to get the top view a1,b1c1d1, etc., smaller than the true shape and size. 5. Reproduce the top view a1, b1, c1, d1, e1, f1 in such a way that the diagonal a1d1 is inclined to the given angle 60° to VP. 6. Draw horizontal lines from a¢1, b¢1, c¢1, etc., and vertical lines from top view a2, b2, c2, etc., to get the required front view a¢2, b¢2, c¢2, d¢2, e¢2, f ¢2 of the plate smaller than the true shape and size.
90
Lesson Plan for Engineering Graphics
Projections of Planes
91
Problem 7 Draw the projections of a regular pentagon of side 40 mm which has its surface inclined at 30∞ to VP and a side parallel to VP and inclined at 60∞ to HP. Solution In this position, the surface of the plate is inclined to both VP and HP. Its projections are obtained in three steps. Step 1: Assume that the plate has its surface parallel to VP and perpendicular to HP. Draw its front view which will have the true shape and size. Project the top view which will be a line parallel to XY line. Step 2: Reproduce the top view tilted to the given angle f to VP and project the front view of the plane which will be smaller than the true shape and size. Step 3: Reproduce the front view by considering the side of the plate that makes the given angle with HP. Project the top view of the plane which is also smaller than the true shape and size. To draw the projections 1. Draw the front view of the pentagon considering one of the sides perpendicular to XY. Then only while tilting the surface to the required angle with VP, this side of the plane will rest on VP. 2. The top view of the plane is projected and obtained on XY as a line. 3. Tilt and reproduce the top view line to the given angle 30° with XY in such a way that the end a(b) is on the XY line. 4. Draw horizontal lines from front view a, b c, etc and vertical lines from top view a1, b1, c1, etc., to get the front view of the plane which is smaller than the true shape and size. 5. Reproduce the front view in such a way that the side a¢1b¢1 is inclined to the given angle 60° to HP. 6. Draw horizontal lines from a¢1, b¢1, c¢1, etc., and vertical lines from a¢2, b¢2, c¢2, etc., to get the required top view of the pentagon plate which is smaller than the true shape and size.
92
Lesson Plan for Engineering Graphics
Projections of Planes
93
Problem 8 Draw the projections of a regular hexagon of side 25 mm, having one of its sides on the ground and inclined at 60∞ to VP and its surface making an angle of 45∞ with the ground. Solution In this position, the surface of the plate is inclined to both HP and VP, its projections are obtained in three steps. Step 1: Assume that the plane has its surface parallel to HP and perpendicular to VP. Draw its top view which will have the true shape and size. Project the front view which will be a line parallel to the XY line. Step 2: Reproduce the front view tilted to the given angle q to HP and project the top view of the plane which will be smaller than the true shape and size. Step 3: Reproduce the top view by considering the side of the plate that makes, the given angle with VP. Project the front view of the plane which is also smaller than the true shape and size. To draw the projections 1. Draw the top view of the hexagon considering one of the sides is perpendicular to XY. Then only while tilting the surface to the required angle with HP, this side of the plane will rest on HP. 2. The front view of the plane is projected and obtained on XY as a line (a)¢b¢(f ¢)c¢(e¢)d¢. 3. Tilt and reproduce the front view (a¢)b¢(f ¢)c¢(e¢)d¢ to the given angle 45° with XY in such a way that the end (a¢)b¢ is on XY line. 4. Draw horizontal lines from top view a, b, c etc and vertical lines from front view a¢1, b¢1, c¢1, etc., to get the top view a¢1,b¢1,c¢1,d¢1,e¢1,f ¢1, smaller than the true shape and size. 5. Reproduce the top view a1, b1, c1, d1, e1, f1, in such a way that the side a1, b1 is inclined to the given angle 30° to VP. 6. Draw horizontal lines from a¢1, b¢1, c¢1 etc and vertical lines from top view a1, b1, c1, etc., to get the required front view a¢2,b¢2,c¢2,d¢2,e¢2,f ¢2 of the plate smaller than the true shape and size.
94
Lesson Plan for Engineering Graphics
Space for Rough Work