Tabla De Transformadas De Laplace 4j6zm
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3b7i
Overview 3e4r5l
& View Tabla De Transformadas De Laplace as PDF for free.
More details w3441
- Words: 489
- Pages: 4
Propiedades Linealidad
Derivación
Integración
Dualidad
Desplazamiento de la frecuencia
Desplazamiento temporal
Nota:
es la función escalón unitario.
Desplazamiento potencia n-ésima
Convolución
Transformada de Laplace de una función con periodo p
Condiciones de convergencia
(que crece más rápido que función de orden exponencial de ángulos.
) no pueden ser obtenidas por Laplace, ya que
Teorema del valor inicial Sea una función
derivable a trozos y que
Entonces :
es el conjunto de funciones continuas a trozos con orden exponencial. Teorema del valor final Sea
una función derivable a trozos tal que
.Entonces :
es el conjunto de funciones continuas a trozos con orden exponencial.
, es una
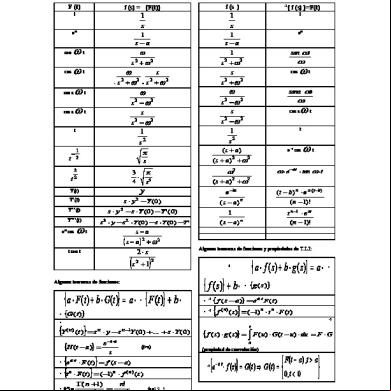
Tabla de las transformadas de Laplace más comunes La siguiente tabla provee la mayoría de las transformaciones de Laplace para funciones de una sola variable. Debido a que la transformada de Laplace es un operador lineal, la transformada de Laplace de una suma es la suma de la transformada de Laplace de cada término.
Aquí está una lista de las transformadas más comunes. En ella denota a la llamada función de Heaviside o función escalón, que vale 1 cuando su argumento es positivo y 0 cuando su argumento es negativo. Cuando su argumento vale 0 se le suele asignar el valor 1/2, aunque esto no tiene relevancia práctica.
ID
Función
1
retraso ideal
1a
impulso unitario
2
enésima potencia retrasada y con desplazamiento en la frecuencia
2a n-ésima potencia
2a.1 q-ésima potencia
2a.2 escalón unitario
2b
escalón unitario con retraso
2c
Rampa
2d
potencia n-ésima con cambio de frecuencia
2d.1
amortiguación exponencial
3
convergencia exponencial
3b
exponencial doble
4
seno
5
coseno
5b
Seno con fase
6
seno hiperbólico
Dominio en el tiempo
Dominio en la frecuencia
Región de la convergencia para sistemas causales
coseno hiperbólico
7
8
9
onda senoidal con amortiguamiento exponencial onda cosenoidal con amortiguamiento exponencial
10
raíz n-ésima
11 logaritmo natural Función de Bessel de primer tipo, de orden n Función de Bessel modificada de primer tipo, de orden n Función de Bessel de segundo tipo, de orden 0 Función de Bessel modificada de segundo tipo, de orden 0
12
13
14
15
16 Función de error Notas explicativas:
representa la función escalón unitario.
, un número real, típicamente representa tiempo, aunque puede representar cualquier variable independiente. es la frecuencia angular compleja.
representa la Delta de Dirac. representa la función gamma.
,
es un número entero.
,
,y
son números reales.
es la constante de EulerMascheroni.
sistema causal es un sistema donde la respuesta al impulso h(t) es cero para todo tiempo t anterior a t = 0. En general, el ROC para sistemas causales no es el mismo que el ROC para sistemas anticausales. Véase también causalidad.
Relación con otras transformadas La transformada de Laplace está estrechamente relacionada con la Transformada de Fourier y la Transformada Z (véase por ejemplo: Relación de la transformada Z con la transformada de Laplace).
Derivación
Integración
Dualidad
Desplazamiento de la frecuencia
Desplazamiento temporal
Nota:
es la función escalón unitario.
Desplazamiento potencia n-ésima
Convolución
Transformada de Laplace de una función con periodo p
Condiciones de convergencia
(que crece más rápido que función de orden exponencial de ángulos.
) no pueden ser obtenidas por Laplace, ya que
Teorema del valor inicial Sea una función
derivable a trozos y que
Entonces :
es el conjunto de funciones continuas a trozos con orden exponencial. Teorema del valor final Sea
una función derivable a trozos tal que
.Entonces :
es el conjunto de funciones continuas a trozos con orden exponencial.
, es una
Tabla de las transformadas de Laplace más comunes La siguiente tabla provee la mayoría de las transformaciones de Laplace para funciones de una sola variable. Debido a que la transformada de Laplace es un operador lineal, la transformada de Laplace de una suma es la suma de la transformada de Laplace de cada término.
Aquí está una lista de las transformadas más comunes. En ella denota a la llamada función de Heaviside o función escalón, que vale 1 cuando su argumento es positivo y 0 cuando su argumento es negativo. Cuando su argumento vale 0 se le suele asignar el valor 1/2, aunque esto no tiene relevancia práctica.
ID
Función
1
retraso ideal
1a
impulso unitario
2
enésima potencia retrasada y con desplazamiento en la frecuencia
2a n-ésima potencia
2a.1 q-ésima potencia
2a.2 escalón unitario
2b
escalón unitario con retraso
2c
Rampa
2d
potencia n-ésima con cambio de frecuencia
2d.1
amortiguación exponencial
3
convergencia exponencial
3b
exponencial doble
4
seno
5
coseno
5b
Seno con fase
6
seno hiperbólico
Dominio en el tiempo
Dominio en la frecuencia
Región de la convergencia para sistemas causales
coseno hiperbólico
7
8
9
onda senoidal con amortiguamiento exponencial onda cosenoidal con amortiguamiento exponencial
10
raíz n-ésima
11 logaritmo natural Función de Bessel de primer tipo, de orden n Función de Bessel modificada de primer tipo, de orden n Función de Bessel de segundo tipo, de orden 0 Función de Bessel modificada de segundo tipo, de orden 0
12
13
14
15
16 Función de error Notas explicativas:
representa la función escalón unitario.
, un número real, típicamente representa tiempo, aunque puede representar cualquier variable independiente. es la frecuencia angular compleja.
representa la Delta de Dirac. representa la función gamma.
,
es un número entero.
,
,y
son números reales.
es la constante de EulerMascheroni.
sistema causal es un sistema donde la respuesta al impulso h(t) es cero para todo tiempo t anterior a t = 0. En general, el ROC para sistemas causales no es el mismo que el ROC para sistemas anticausales. Véase también causalidad.
Relación con otras transformadas La transformada de Laplace está estrechamente relacionada con la Transformada de Fourier y la Transformada Z (véase por ejemplo: Relación de la transformada Z con la transformada de Laplace).