Aceleracion Radial Y Tangencial 4e558

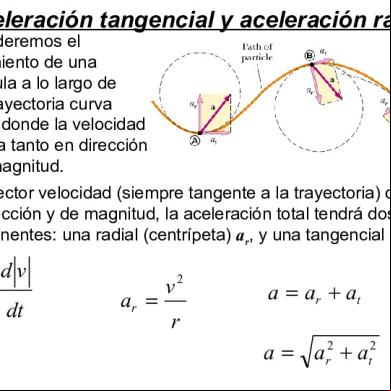
Aceleración tangencial y aceleración radial

Consideremos el movimiento de una partícula a lo largo de una trayectoria curva suave donde la velocidad cambia tanto en dirección y en magnitud.

Si el vector velocidad (siempre tangente a la trayectoria) cambia de dirección y de magnitud, la aceleración total tendrá dos componentes: una radial (centrípeta) ar, y una tangencial at

at 

 dv dt

ar 

v

2

   a  ar  at

r

a a a 2 r

2 t

Ej: La figura representa la aceleración total de una partícula en movimiento hacia la derecha en un círculo de radio de 2,50 m en un cierto instante de tiempo. En este instante, encontrar (a) la aceleración radial, (b) la velocidad de la partícula, y (c) su aceleración tangencial. Solución: a) La aceleración radial o centrípeta es aquella que se encuentra dirigida hacia el centro de la trayectoria circular, para determinar ésta se debe descomponer el vector aceleración en sus componentes :

b) La relación que existe entre la aceleración radial (o centrípeta) y la velocidad tangencial es:



c) Para determinar la magnitud de la aceleración tangencial se debe tener en cuenta que la magnitud de la aceleración total está dada por: