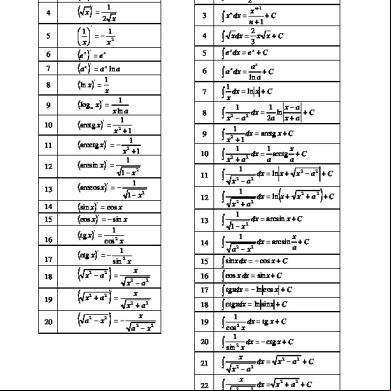
Tabel Derivate 2p1z6r

Formula de derivare

( c )' =0 ( c ∈ R )

Mulţimea valorilor lui x pe care este adevărată R

'

( 0, ∞ )

'

R

( x α ) =α x α −1 ( α ∈ R )

( x n ) =n x n−1 ( n ∈ N ¿ ) '

( x m ) =m xm −1 ( m∈ Z , m< 0 ) 1

'

n

(√ x ) =

n

n √ x n−1

( n ∈ N , n ≥2 )

¿ R {0 ¿ ¿ ¿ R {0 ¿ ¿ , n impar

( 0, ∞ ) , n par

'

( a x ) =a x ∙ ln a ( a> 0, a≠ 1 ) x '

( e ) =e

R

x

1

'

( log a x ) = x ln a ( a>0, a ≠ 1 ) 1 ( ln x ) = x

( 0, ∞ )

'

( sin x )' =cos x

R

( cos x )' =−sin x

R

1 ( tg x ) = 2 =1+tg 2 x cos x

¿ π R { ( 2 k +1 ) k ∈ Z ¿ ¿ 2

'

( ctg x )' =

1 =−( 1+ ctg 2 x) 2 sin x

|

¿ R {kπ|k ∈ Z ¿ ¿

( arcsin x ) '=

1 √ 1−x 2

(−1,1 )

( arccos x )' =

−1 √ 1−x 2

(−1,1 )

( arctg x )' =

1 1+x 2

R

( arcctg x )' =

−1 1+ x 2

R

TABELUL FORMULELOR UZUALE DE DERIVARE

TABLELUL DERIVATELOR FUNCŢIILOR COMPUSE '

( uα ) =α uα −1 ∙ u' '

( au ) =au ∙ ln a∙ u ' u'

( tgu )' =

u' 2 =1+tg u∙ u ' 2 cos u

( ctgu )' =

u' =−( 1+ ctg 2 u)∙ u ' 2 sin u

( arcsin u ) ' =

u' √1−u2

u' u

( arccos u )' =

−u ' √1−u 2

( sin u )' =cos u ∙ u'

( arctg u )' =

( cos u )' =−sin u ∙u '

( arcctg u )' =

'

( loga u ) = u ln a ( ln u )' =

u' 2 1+u −u ' 1+u2