Copy Of Learning Competency Directory 1s1y

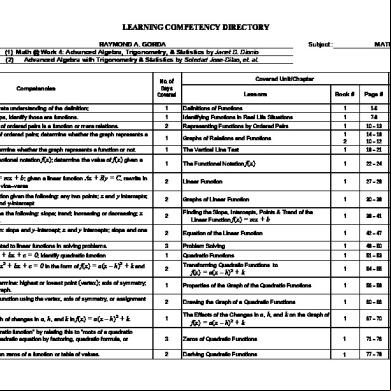
LEARNING COMPETENCY DIRECTORY Teacher's Name: Reference Used:

RAYMOND A. GORDA (1) Math @ Work 4: Advanced Algebra, Trigonometry, & Statistics by Janet D. Dionio (2) Advanced Algebra with Trigonometry & Statistics by Soledad Jose-Dilao, et. al.

MATHEMATICS IV

Covered Unit/Chapter

No. of Days Covered

Competencies

Subject::

Lessons

Target Activities Book #

Page #

Letter/ No.

Book #

Page #

Define a function and demonstrate understanding of the definition;

1

Definitions of Functions

1

1-6

A–D

1

2–6

Given some real life relationships, identify those are functions.

1

Identifying Functions in Real Life Situations

1

7-9

A–C

1

8–9

Determine whether a given set of ordered pairs is a function or mere relations.

2

Representing Functions by Ordered Pairs

1

10 – 13

A–C

1

11 – 13

14 – 18 10 – 12

A–B

1

14 – 16

Draw the graph of a given set of ordered pairs; determine whether the graph represents a function or a mere relation.

1

Graphs of Relations and Functions

1 2

Use the vertical line test to determine whether the graph represents a function or not.

1

The Vertical Line Test

1

19 – 21

A–B

1

20 – 21

Illustrate the meaning of the functional notation f(x); determine the value of f(x) given a value for x.

1

The Functional Notation f(x)

1

22 – 24

A–B

1

23

Define the linear function f(x) = mx + b; given a linear function Ax the form of f(x) = mx + b and vice–versa

2

Linear Function

1

27 – 29

A–C

1

28 – 29

Draw the graph of a linear function given the following: any two points; x and y intercepts; slope and one point; or slope and y-intercept

2

Graphs of Linear Function

1

30 – 38

A–E

1

31 – 38

Given f(x) = mx + b, determine the following: slope; trend; increasing or decreasing; x and y intercept; or some points.

2

Finding the Slope, Intercepts, Points & Trend of the Linear Function f(x) = mx + b

1

39 – 41

A–C

1

40 – 41

Determine f(x) = mx + point; or any two points

2

Equation of the Linear Function

1

42 – 47

A–F

1

43 – 47

3

Problem Solving

1

48 – 50

1

49 – 50

1

Quadratic Functions

1

51 – 53

A–C

1

52 – 53

1

54 – 55

A, B

1

55

A, B

1

57 – 59

1

62 – 66

+ By = C, rewrite in

b given: slope and y-intercept; x and y intercepts; slope and one

Apply knowledge and skills related to linear functions in solving problems. Define a quadratic function ax

2

+ bx + c = 0; identify quadratic function Rewrites a quadratic function ax2 + bx + c = 0 in the form of f(x) = a(x – h)2 + k and vice–versa

2

Transforming Quadratic Functions to

f(x) = a(x – h)2 + k

Given a quadratic function, determine: highest or lowest point (vertex); axis of symmetry; or direction of opening of the graph.

1

Properties of the Graph of the Quadratic Functions

1

56 – 59

Draw the graph of a quadratic function using the vertex, axis of symmetry, or assignment of points.

2

Drawing the Graph of a Quadratic Functions

1

60 – 66

1

67 – 70

A–C

1

68 – 70

The Effects of the Changes in a, h, and k on the Graph of

= a(x – h)2 + k.

1

Determine the “zeros of a quadratic function” by relating this to “roots of a quadratic equation”; find the roots of a quadratic equation by factoring, quadratic formula, or completing the square.

3

Zeros of Quadratic Functions

1

71 – 76

A–D

1

73 – 76

Derive a quadratic function given zeros of a function or table of values.

2

Deriving Quadratic Functions

1

77 – 79

A–C

1

78 – 79

Analyze the effects on the graph of changes in a, h, and k in f(x)

f(x) = a(x – h)2 + k

Apply knowledge and skills related to quadratic functions and equations in problem solving.

3

Application of Quadratic Functions

1

80 – 83

Review the definition of polynomials; identify a polynomial from a list of algebraic expressions.

1

Polynomials

1

91 – 94

Define a polynomial function; identify a polynomial function from a given set of relations; determine the degree and number of of a given polynomial function

3

Polynomial Functions

1

Find the quotient of polynomials by algorithm & synthetic division; find by synthetic division the quotient and the remainder when p(x) is divided by (x – c)

3

Division of Polynomials

State and illustrate the Remainder Theorem; find the value of p(x) for x division or remainder theorem; state and illustrate the factor theorem

4

Find the zeros of polynomial functions of degree greater than 2 by factor theorem, factoring, synthetic division, or depressed equations.

1

81 – 83

A–D

1

92 – 94

95 – 100

A–F

1

97 – 100

1

101 – 105

A–D

1

103 – 105

The Remainder Theorem & the Factor Theorem

1

106 – 109

A–D

1

108 – 109

3

Zeros of Polynomial Functions of Degree Greater than 2

1

113 – 117

A–D

1

116 –117

Identify certain relationships in real life which are exponential; define the exponential function f(x) = ax and differentiate it from other functions; given a table of ordered pairs, state whether the trend is exponential or not

2

Definition of Exponential Functions

1

122 – 126

A–C

1

123 – 126

Draw the graph of an exponential function f(x) = ax ; describe some properties of the exponential function or its graph; given the graph of an exponential function determine the domain, range, intercepts, trend, & asymptote

2

Properties of Exponential Function & Its Graph

1

135 – 138

A–E

1

136 – 138

Use the laws on exponents to find the zeros of exponential functions

2

Laws of Exponents

1

139 – 141

A–D

1

140 – 141

Define inverse functions; determine the inverse of a given function

2

Inverse Functions/Relations

1

142 –146

A–D

1

144 –146

Define the logarithmic function f(x) f(x) = ax.

1

The Logarithmic Function

1

147 – 148

A–B

1

148

State the laws for logarithms; apply the laws for logarithms; solve simple logarithmic equations.

4

Laws of Logarithms Application of the Laws of Logarithms

1

150 – 153

A–C

1

152 – 153

Solve problems involving exponential and logarithmic functions.

3

Application of Exponential and Logarithmic Functions

1

154 – 156

A

1

155 – 156

Define unit circle, arc lengths, & unit measures of an angle; convert from degree to radian and vice–versa.

3

The Unit Circle

1

157 – 159

A–C

1

158 – 159

Illustrates angles in standard position, coterminal angles, & reference angle.

3

Angles in Standard Position

1

160 – 162

A–C

1

161 – 162

Visualize rotations along the unit circle and relate these to angle measures (clockwise or counterclockwise directions): length of an arc, angles beyond 360o or 2π radians

2

Rotations Along the Unit Circle

1

163 – 165

A–B

1

163 – 165

Given an angle in standard position in a unit circle, determine the coordinates of the point of intersection of the unit circle and the terminal side.

3

Coordinates of the Point of Intersection of the Unit Circle and the Terminal Side

1

170 – 171

A–E

1

170 – 171

Define sine functions; state the sine of an angle; define cosine functions; state the cosine of an angle

3

The Sine Function & the Cosine Function of Special Number

1

172 – 175

A–C

1

173 – 175

Define tangent function and other circular functions; state the tangent and other circular functions of an angle

4

The Tangent Function and Other Circular Functions of θ. Use of Calculator to Get sin θ, cos θ, & tan θ.

1

176 – 181

A–D

1

177 – 181

Describe the properties of the graphs of sine, cosine, & tangent functions.

2

Graphs of Sine, Cosine, & Tangent Functions

1

182 – 183

A–D

1

183

State the fundamental trigonometric identities and use these identities to solve other identities.

2

The Eight Fundamental Identities

1

184 – 186

A–E

1

185 – 186

Solve simple trigonometric equations.

2

Simple Trigonometric Equations

2

240 – 243

5–9

2

243

Solve problems involving right triangles.

3

Solving Right Triangle Applications of the Trigonometric Functions

2

246 – 247 248 – 250

1–5 1–5

2

247 249 – 250

= k by synthetic

= loga x as the inverse of the exponential function

Solve problems involving triangles using the sine law.

2

The Law of Sine

2

250 – 253

2

257 – 258

Solve problems involving triangles using the cosine law.

2

The Law of Cosine

2

254 – 258

2

257 – 258

Define statistics, sample, & population; give the importance of the study of statistics

2

Statistics Defined

2

264 – 267

2

266 – 267

State and explain the different sampling techniques

2

Sampling

2

267 – 272

2

272

Analyze, Interpret accurately, and draw conclusion from graphic and tabular presentation of statistical data

4

Organizing Data Table & Graphs

2

273 – 280

2

275, 278, 279, 281

Construct frequency distribution table

2

Frequency Distribution

2

282 – 285

2

284 – 285

Use the rules of summation to find sums

2

Summation

2

286 – 289

2

289

Find the arithmetic mean, grouped & ungrouped

3

The Mean

2

290 – 294

2

294

Find the median, grouped & ungrouped

4

The Median

2

295 – 298

2

298

Find the mode, grouped & ungrouped

2

The Mode

2

299 – 301

2

300 – 301

calculate the different measures of variability relative to a given set of data, grouped or ungrouped, range & standard deviation; give the characteristics of a set of data using the measures of variability

5

Measures of Variability

2

302 – 307

2

303, 305, 307

from a given statistical data, analyze, interpret, draw conclusions, make predictions, and make recommendations / decisions.

4

Analyzing Data Set

2

308 – 311

2

310 – 311