Cómo Hacer El Péndulo Dibujante 6z6l3x

Cómo hacer el péndulo dibujante

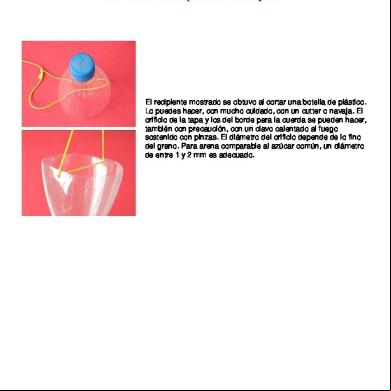
El recipiente mostrado se obtuvo al cortar una botella de plástico. Lo puedes hacer, con mucho cuidado, con un cutter o navaja. El orificio de la tapa y los del borde para la cuerda se pueden hacer, también con precaución, con un clavo calentado al fuego sostenido con pinzas. El diámetro del orificio depende de lo fino del grano. Para arena comparable al azúcar común, un diámetro de entre 1 y 2 mm es adecuado.

Las cuerdas se sujetan de dos puntos altos en un soporte firme, puede ser el marco de una puerta o el techo. Para obtener figuras de Lissajous buenas la amplitud máxima no debe ser muy grande, por ejemplo, para una longitud de 2 m, es buena una amplitud, o ancho de oscilación, de unos 10 o 15 cm. Por eso es mejor que la longitud total de la cuerda sea grande, desde el techo hasta el piso es posible una longitudL1 de aproximadamente 2.5 m. Lo anterior también es porque no conviene que L2 sea muy corta, pues si es así su amplitud también se ve reducida y los trazos no se aprecian bien. Se debe cuidar que el nudo en donde se unen las tres cuerdas que forman la Y sea muy firme y no sea corredizo.

Las longitudes y los periodos El periodo de un péndulo es proporcional a la raíz cuadrada de su longitud, entonces podemos decir que la longitud es proporcional al cuadrado del periodo. Si deseamos que un péndulo haga los trazos 2:1, el periodo en y debe ser doble del periodo en x. La razón de periodos es 2:1, pero la razón de longitudes es el cuadrado de ella, es decir 4:1. Es decir L1 debe ser 4 veces el valor de L2. por ejemplo si L1 es de 2.40 m, L2 es la cuarta parte, 60 cm. Para los trazos 3:2 la razón de longitudes es también el cuadrado de esos números, 9:4. Para L1 de 2.4 m, la longitud L2 es 4/9 de 2.40 m, es de 1.07 m.

De la misma manera, para los trazos 4:3, la longitud de L2 es 9/16 de L1. Para L1 de 2.40 m, L2 es 1.35 m. ¿Puedes hacer las figuras 3:1? Pero ojo, para cualquier configuración lo importante es la razón entre los periodos. Al hacer el péndulo, los valores calculados de longitudes deben tomarse solamente como valores iniciales, los valores definitivos los vas a encontrar por ensayo y error, alargando y acortando las cuerdas hasta que los periodos queden en la razón buscada. Puedes usar un cronómetro para medir los periodos y una calculadora para encontrar la razón entre ellos. Recuerda que para aumentar la razón hay que acortar L2 sin cambiar L1, pero eso sí implica alargar la cuerda superior, la que tiene forma de V. ¡Paciencia! Eso es porque los cálculos mostrados están basados en la suposición de que tenemos un péndulo simple idealizado, de cuerda sin masa y un objeto pequeñito suspendido con oscilaciones en x independientes de las de y. En realidad la cuerda tiene masa, el recipiente no es tan pequeño y las oscilaciones en x y y no son tan independientes.

Sitúa un papel grande debajo del péndulo para que ahí caiga la arena y sea fácil recuperarla y volver a utilizarla. Si obtienes un trazo como el de esta foto es porque el recipiente queda vibrando al soltarlo. Si deseas trazos sin vibración deberás ensayar con paciencia hasta lograrlos. La arena fina se puede comprar en algunos almacenes que venden artículos para acuarios. Cuida que esté seca y no tenga mezclados granos grandes que obstruyan el orificio de salida.

Y por supuesto que no tienes por qué restringirte a razones enteras de periodos. Puedes hacer variaciones al péndulo y hacer otros trazos, algunos más raros de los que se ven aquí COMO HACER UN PENDULO DIBUJANTE

OBJETIVO: Observar que el movimiento pendular se encuentra relacionado con la fuerza de la gravedad y que su velocidad depende del impulso que este recibe FUNDAMENTACION CIENTIFICA: El movimiento de un péndulo se relaciona con la cinemática y la dinámica, debido a que estudia el movimiento y las cusas que lo originan. Este movimiento fue estructurado por primera vez por Galileo Galiley, es el cual se Construyo varios péndulos para demostrar sus razonamientos. 50 años después Huygens aplico el movimiento pendular al movimiento de los relojes. 100 años después León Fucalt descubre que el movimiento pendular se debe principalmente al movimiento de rotación de la tierra • Elementos del movimiento pendular: • Longitud del péndulo: es la longitud del hilo. Se mide desde el punto de suspensión hasta el centro de gravedad del cuerpo que oscila. • Oscilación: es el movimiento realizado por el péndulo desde una de sus posiciones extremas hasta otra y su vuelta hasta la primera posición. •

Período: es el tiempo que emplea el péndulo en realizar una oscilación. • Amplitud: es el ángulo formado por la vertical con el hielo, cuando el péndulo está en una de sus posiciones externa

COMO HACER UN PENDULO DIBUJANTE

MATERIALES: PARTE SUPERIOR DE UNA BOTELLA PLASTICA CON TAPA PEDAZOS DE PIOLA, HOJA DE PAPEL UN CLAVO PEQUEÑO TRES VARILLAS METALICAS DOS TRIPODE DOS NUECES DOBLE ARENA O CEMENTO BLANCO PROCEDIMIENTO: 1 RECOSTRAR LA PARTE SUPERIOR DE LA BOTELLA 2 CON EL CLAVO HACER UNA PERFORECION EN EL CENTRO DE LA TAPA Y OTRA EN LOS EXTREMOS DE LA PARTE SUPERIOR 3 COLOCAR LA PIOLA EN LAS PERFORACIONES DE LA PARTE SUPERIOR.

4 UNIR EL TRIPODE, LAS VARILLAS Y LA NUEZ DOBLE 5 COLOCAR ARENA EN EL CONO Y SUJETARLO A LA VARILA 6. DAR UN LIJERO MOVIMIENTO Y OBSERVAR

Péndulo simple o matemático Artículo principal: Péndulo simple

Componentes del peso de la masa pendular.

También llamado péndulo ideal, está constituido por un hilo inextensible de masa despreciable, sostenido por su extremo superior de un punto fijo, con una masa puntual sujeta en su extremo inferior que oscila libremente en un plano vertical fijo. Al separar la masa pendular de su punto de equilibrio, oscila a ambos lados de dicha posición, desplazándose sobre una trayectoria circular con movimiento periódico. [editar]Ecuación

del movimiento

Para escribir la ecuación del movimiento, observaremos la figura adjunta, correspondiente a una posición genérica del péndulo. La flecha azul representa el peso de la masa pendular. Las flechas en color violeta representan las componentes del peso en las direcciones tangencial y normal a la trayectoria. Aplicando la Segunda ley de Newton en la dirección del movimiento, tenemos

donde el signo negativo tiene en cuenta que la tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura). Considerando la relación existente entre la aceleración tangencial y la aceleración angular

obtenemos finalmente la ecuación diferencial del movimiento plano del péndulo simple

[editar]Período

de oscilación

Factor de amplificación del período de un péndulo, para una amplitud angular cualquiera. Para ángulos pequeños el factor vale aproximadamente 1 pero tiende a infinito para ángulos cercanos a π (180º).

El astrónomo y físico italiano Galileo Galilei, observó que el periodo de oscilación es independiente de la amplitud, al menos para pequeñas oscilaciones. En cambio, éste depende de la longitud del hilo. El período de la oscilación de un péndulo simple restringido a oscilaciones de pequeña amplitud puede aproximarse por:

Para oscilaciones mayores la relación exacta para el período no es constante con la amplitud e involucra integrales elípticas de primera especie:

Donde φ0 es la amplitud angular máxima. La ecuación anterior puede desarrollarse en serie de Taylor obteniéndose una expresión más útil: