Medidas De Dispersion Rango,varianza, Desvstnd 326553
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3b7i
Overview 3e4r5l
& View Medidas De Dispersion Rango,varianza, Desvstnd as PDF for free.
More details w3441
- Words: 422
- Pages: 2
SAN ROMAN ESQUITIN ALFREDO JAIRO PROBABILIDAD Y ESTADISTICA ¿QUE ES UNA MEDIDAD DE DISPERSION? Y FORMULAS PARA CALCULAR: RANGO, VARIANZA Y DESVIACION ESTANDAR
INTRODUCCION: Cuando se indican ciertos aspectos del conjunto de datos que no nos lo dicen las medidas de tendencia central; es decir cuando se busca una descripción más completa de la naturaleza de un conjunto de datos se obtiene cuando se utiliza tanto las medidas de tendencia central así como las de variabilidad dispersión.
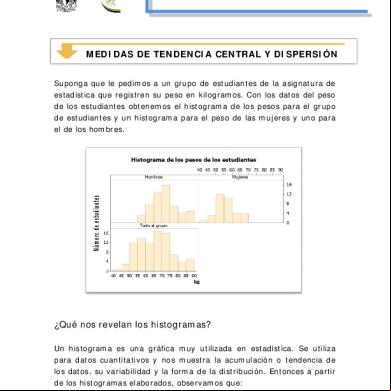
DESARROLLO TEMATICO: Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la mediana media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la mediana media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos. Existen varias medidas de variabilidad las más importantes a continuación: Rango Varianza Desviación estándar
Rango: Se calcula hallando la diferencia (resta) entre los valores máximo y mínimo Rango = R = Valor máximo – Valor mínimo
Varianza: Es una medida de variabilidad que se obtiene elevando al cuadrado la desviación estándar. Se simboliza por s2.
SAN ROMAN ESQUITIN ALFREDO JAIRO PROBABILIDAD Y ESTADISTICA ¿QUE ES UNA MEDIDAD DE DISPERSION? Y FORMULAS PARA CALCULAR: RANGO, VARIANZA Y DESVIACION ESTANDAR
Desviación estándar Es la medida de variabilidad más adecuada por sus propiedades algebraicas, se le conoce también como desviación típica. Este se utiliza para valorar la diferencia entre un dato y el valor de la media del conjunto de datos. Es una especie de desviación promedio con respecto a la media. A continuación su fórmula para calcularla.
Dónde: X= Valores de los datos = Media = Numero de datos
Para calcular la desviación estándar se procede de la siguiente manera: 1. Calcular el valor de la media 2. Restar la media de cada valor individual para tener una lista de desviaciones de la forma 3. 4. 5. 6.
Elevar al cuadrado cada una de las diferencias Sumar todos los resultados obtenidos en el paso anterior Dividir el total entre el número de datos Calcular la raíz cuadrada del resultado anterior
CONCLUSION: Las medidas de dispersión son importantes porque nos proporcionan información adicional que nos permite juzgar la confiabilidad de nuestra medida es decir si los datos se encuentran muy dispersos. Además de que existen problemas característicos para datos muy dispersos
BIBLIOGRAFIA: Luis Carlos Castillo Valderas & Jesús Lozada Hernández, (2009) Probabilidad y estadística I, Mexico, Pág.116-122 http://es.wikipedia.org/wiki/Medidas_de_dispersi%C3%B3n
INTRODUCCION: Cuando se indican ciertos aspectos del conjunto de datos que no nos lo dicen las medidas de tendencia central; es decir cuando se busca una descripción más completa de la naturaleza de un conjunto de datos se obtiene cuando se utiliza tanto las medidas de tendencia central así como las de variabilidad dispersión.
DESARROLLO TEMATICO: Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la mediana media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la mediana media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos. Existen varias medidas de variabilidad las más importantes a continuación: Rango Varianza Desviación estándar
Rango: Se calcula hallando la diferencia (resta) entre los valores máximo y mínimo Rango = R = Valor máximo – Valor mínimo
Varianza: Es una medida de variabilidad que se obtiene elevando al cuadrado la desviación estándar. Se simboliza por s2.
SAN ROMAN ESQUITIN ALFREDO JAIRO PROBABILIDAD Y ESTADISTICA ¿QUE ES UNA MEDIDAD DE DISPERSION? Y FORMULAS PARA CALCULAR: RANGO, VARIANZA Y DESVIACION ESTANDAR
Desviación estándar Es la medida de variabilidad más adecuada por sus propiedades algebraicas, se le conoce también como desviación típica. Este se utiliza para valorar la diferencia entre un dato y el valor de la media del conjunto de datos. Es una especie de desviación promedio con respecto a la media. A continuación su fórmula para calcularla.
Dónde: X= Valores de los datos = Media = Numero de datos
Para calcular la desviación estándar se procede de la siguiente manera: 1. Calcular el valor de la media 2. Restar la media de cada valor individual para tener una lista de desviaciones de la forma 3. 4. 5. 6.
Elevar al cuadrado cada una de las diferencias Sumar todos los resultados obtenidos en el paso anterior Dividir el total entre el número de datos Calcular la raíz cuadrada del resultado anterior
CONCLUSION: Las medidas de dispersión son importantes porque nos proporcionan información adicional que nos permite juzgar la confiabilidad de nuestra medida es decir si los datos se encuentran muy dispersos. Además de que existen problemas característicos para datos muy dispersos
BIBLIOGRAFIA: Luis Carlos Castillo Valderas & Jesús Lozada Hernández, (2009) Probabilidad y estadística I, Mexico, Pág.116-122 http://es.wikipedia.org/wiki/Medidas_de_dispersi%C3%B3n